Two inclined frictionless tracks , one gradual and the other steep meet at A from where two stones are allowed to slide down from rest , one on each track as shown in figure . Will the stones reach there with the same speed ? Explain . Given θ1=30∘,θ2=60∘andh=10m What are the speeds and times taken by the two stones ?
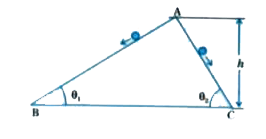Solution in Gujrati
No suppose at time t1 reached at ground
∴ From equation of motion
v=v0+>1,v0=0andg=gccos60∘
∴ t1=vg×12=2×14.1410=2×√2×1010=2√2s
Suppose at time t2 ball - 2 reaches at ground ,
∴Inv=v0+gt2,v0,g=gcos∘
∴v=gcos30∘t2
∴t2=vgcos30∘=2√2×1010×√3=2√2√3
Both balls having time to reach at ground and hence they cannot reached together . Yes , bot balls are released drom height h = 10 cm .
potential energy at height h = kinetic energy at bottom .
∴mgh=12mv2
∴gh=v2
∴v=√2gh
For both ball g and h are unchaned and the speed of balls at the bottom is same .
∴v=√10×10×2
∴v=10√2=10×1.414=14.14ms−1
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - KUMAR PRAKASHANCHAPTER - WORK, ENERGY AND POWER EXERCISE - SECTION - B Numericals (Numerical From .DARPAN. Based On Textbook)
15 Videos
- WORK, ENERGY AND POWER BOOK - KUMAR PRAKASHANCHAPTER - WORK, ENERGY AND POWER EXERCISE - SECTION - C Objective Questions (VSQs)
52 Videos
- WORK, ENERGY AND POWER BOOK - KUMAR PRAKASHANCHAPTER - WORK, ENERGY AND POWER EXERCISE - SECTION - B Numericals (Numerical From Textual Illustration)
29 Videos
- WAVESBOOK - KUMAR PRAKASHANCHAPTER - WAVESEXERCISE - SECTION-F (Questions From Module) (Sample questions for preparation of competitive exams)
23 Videos
Similar Questions
A body while being acted upon by a force →F(x)=(3x2−2x+7)ˆi N gets displaced from x = 0 to x = 10 m in the direction of X -axis .Find the work done [∫xndx=xn+1n+1]
View SolutionIf →A=2ˆi−2ˆjand→B=2ˆk then →A.→B……
View SolutionFind the angle between force →F=(3ˆi+4ˆj−5ˆk) unit and displacement →d=(5ˆi+4ˆj+3ˆk) unit , Also find the projection of F on d .
View SolutionIn a standing wave formed by two atoms separated by 1.21Å, there are 3 nodes and 2 antinodes. Find its wavelength.
View SolutionTwo inclined frictionless tracks, one gradual and the other steep meet at O, from where two stones are allowed to slide down from rest, one on each track. Will the stones reach the bottom at the same time ? Will they reach there with the same speed ? Explain.
View SolutionTwo inclined frictionless tracks, one gradual and the other steep meet at a from where two stones are allowed to slide down from rest, one on each track as shown in Figure. Which of the following statement is correct ?
.
View SolutionTwo inclined frictionless tracks , one gradual and the other sleep meet at A from where two stones are allowed to slide down from rest. One on each track as shown in figure. Which of the following statement is correct?
View SolutionTwo inclined frictionless tracks, one gradual and the other steep meet at A from where to stones are allowed to slide down from rest, one on each track (fig.) Will hte stones reach the bottom at the same time? Will they reach there with the same speed? Explain, given θ1=30∘, θ92)=60∘ and h=10m. What are the speeds and time taken by the two stones?
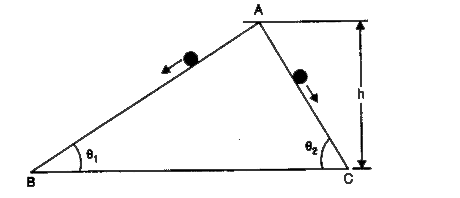
View Solutionदो घर्षणरहित आनत पथ, जिनमे से एक की ढाल अधिक है और दूसरे की ढाल कम है, बिंदु A पर मिलते है। बिंदु A से प्रत्येक पथ पर एक-एक पत्थर को विरामावस्था से नीचे सरकाया जाता है (चित्र)। क्या ये पत्थर एक ही समय पर नीचे पहुँचेंगे? क्या वे वहाँ एक ही चाल से पहुँचेंगे ? व्याख्या कीजिए। यदि θ1=30∘,θ2=60∘ और h=10m दिया है तो दोनों पत्थरों की चाल एवं उनके द्वारा नीचे पहुंचने में लिए गए समय क्या हैं?
View SolutionTwo inclined frictionless tracks, one gradual and the other steep meet at A, from where two stones are allowed to slide down from rest, one on each track. Will the stones reach the bottom at the same time? Will they reach there with the same speed? Given theta_(1)=30^(@),theta_(2)=60^(@),h=10m . What are the speeds and time taken by the two stones?
View Solutionदो घर्षणरहित आनत पथ, जिनमें से एक की ढाल अधिक है और दूसरे की ढाल कम है, बिंदु A पर मिलते हैं । बिंदु A से प्रत्येक पथ पर एक - एक पत्थर को विरामावस्था से नीचे सरकाया जाता है । क्या ये पत्थर एक ही समय पर नीचे पहुँचेंगे ? क्या वे वहाँ एक ही चाल से पहुँचेंगे ? व्याख्या कीजिए । यदि θ1=30∘,θ2=60∘ और h=10m दिया है तो दोनों पत्थरों की चाल एवं उनके द्वारा नीचे पहुँचने में लिए गए समय क्या हैं ?
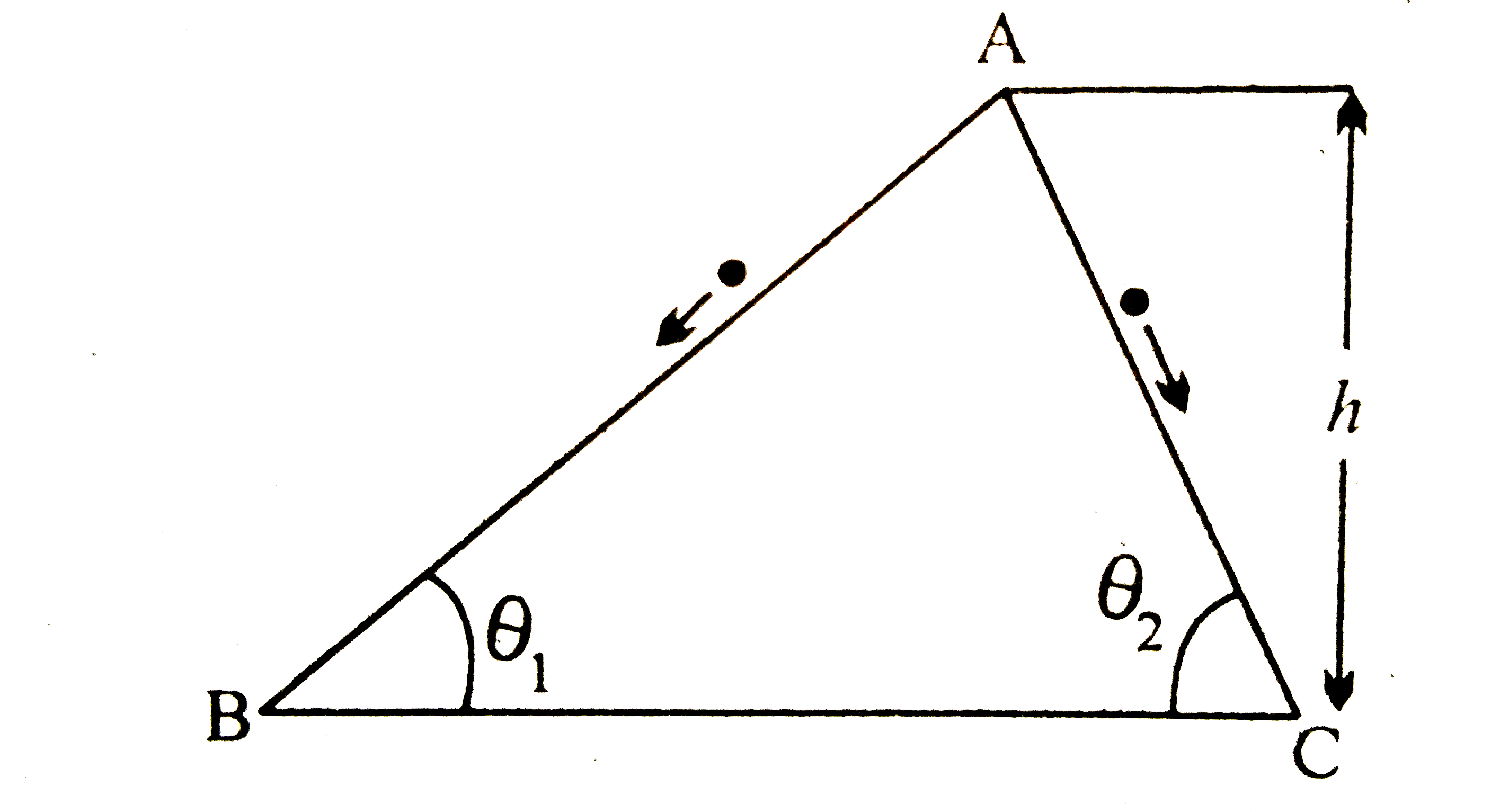
View SolutionTwo inclined frictionless tracks, one gradual and other steep meet at 'A' from where two stones are allowed to slide down from rest, one on each track as shown in figure. The speed of two stones on reaching at bottom are v1andv2 respectively. v1&v2 are related as
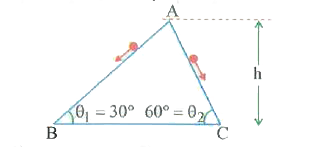
View SolutionTwo inclined frictionless tracks, one gradual and the other steep meet at A from where two stones are allowed to slide down from rest, one on each track (Fig. 6.16). Will the stones reach the bottom at the same time? Will they reach there with the same speed? Explain. Given theta_(1)= 30^(@), theta_(2)= 60^(@)" and "h= 10m , what are the speeds and times taken by the two stones?
View SolutionTwo inclined frictionless tracks, one gradual and the other steep meet at A from where two stones are allowed to slide down from rest, one on each track (Fig. 6.16). Will the stones reach the bottom at the same time? Will they reach there with the same speed? Explain. Given theta_(1)= 30^(@), theta_(2)= 60^(@)" and "h= 10m , what are the speeds and times taken by the two stones?
View SolutionTwo inclined frictionless tracks, one gradual and the other steep meet at A from where to stones are allowed to slide down from rest, one on each track (fig.) Will hte stones reach the bottom at the same time? Will they reach there with the same speed? Explain, given theta_(1)=30^(@) , theta_92)=60^(@) and h=10m. What are the speeds and time taken by the two stones?
View Solution