A particle is projected vertically up and another is let fall to meet at the same instant. If they have velocities equal in magnitude when they meet, the distances travelled by them are in the ratio of
1:1
1:2
3:1
2:3
The correct Answer is:C
Topper's Solved these Questions
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (PARALLELOGRAM LAW, TRIANGLE LAW, POLYGON LAW)
14 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (MOTION IN A PLANE)
20 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A STRAIGHT LINE (HORIZONTAL MOTION)
48 Videos
- RAY OPTICS BOOK - AAKASH SERIESCHAPTER - RAY OPTICS EXERCISE - EXERCISE III
64 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Integer Type Questions
7 Videos
Similar Questions
A particle is projected vertically up and another is let fall to meet at the same instant. If they have velocities equal in magnitude when they meet, the distance travelled by them are in the ratio of
View SolutionA particle is projected vertically upwards with a velocity of 20m/sec. Find the time at which distance travelled is twice the displacement
View Solution
Knowledge Check
A particle is projected vertically upwards from the ground with a speed V and a speed v and a second particle is projected at the same instant from a height h directly above the first particle with the same speed v at an angle of projection θ with the horizontal in upwards direction. The time when the distance between them is minimum is
Ah2υsinθBh2υcosθCh/υDh2υ
A particle is projected vertically upwards from O with a velocity and a second particle is projected at the same instant from P (at a height h above O) with velocity v at an angle of projection θ with the horizontal. Find the time when the distance between them is minimum. Take v=5m/s and h=20m
View SolutionA particle of mass m and charge q is accelerated by a potential difference V volt and made to enter a magnetic field region at an angle θ with the field. At the same moment, another particle of same mass and charge is projected in the direction of the field from the same point. Magnetic field induction is B. What would be the speed of second particle so that both particles meet again and again after regular interval of time. Also, find the time interval after which they meet and the distance travelled by the second particle during that interval.
View SolutionA particle of mass m and charge q is accelerated by a potential difference V volt and made to enter a magnetic field region at an angle θ with the field. At the same moment, another particle of same mass and charge is projected in the direction of the field from the same point. Magnetic field induction is B. What would be the speed of second particle so that both particles meet again and again after regular interval of time. Also, find the time interval after which they meet and the distance travelled by the second particle during that interval.
View SolutionA particle of mass m and charge q is accelerated by a potential difference V volt and made to enter a magnetic field region at an angle θ with the field. At the same moment, another particle of same mass and charge is projected in the direction of the field from the same point. Magnetic field induction is B. What would be the speed of second particle so that both particles meet again and again after regular interval of time. Also, find the time interval after which they meet and the distance travelled by the second particle during that interval.
View SolutionA particle is dropped from a height h and at the same instant another particle is projected vertically up from the ground. They meet when the upper one has descended a height h/3. Find the ratio of their velocities at this instant.
View SolutionTwo paarticles 1 and 2 are projected simultaneusly with velocities v1 and v2, respectively. Particle 1 is projectected vertically up from the top of a cliff of heitht h and particle 2 is projected vertically up from the bottom of the cliff. If the bodies meet (a) above the top of the cliff, (b) between the top and bottom of the the cliff, and (c ) below the bottom of the cliff, find the time of meeting of the particles.
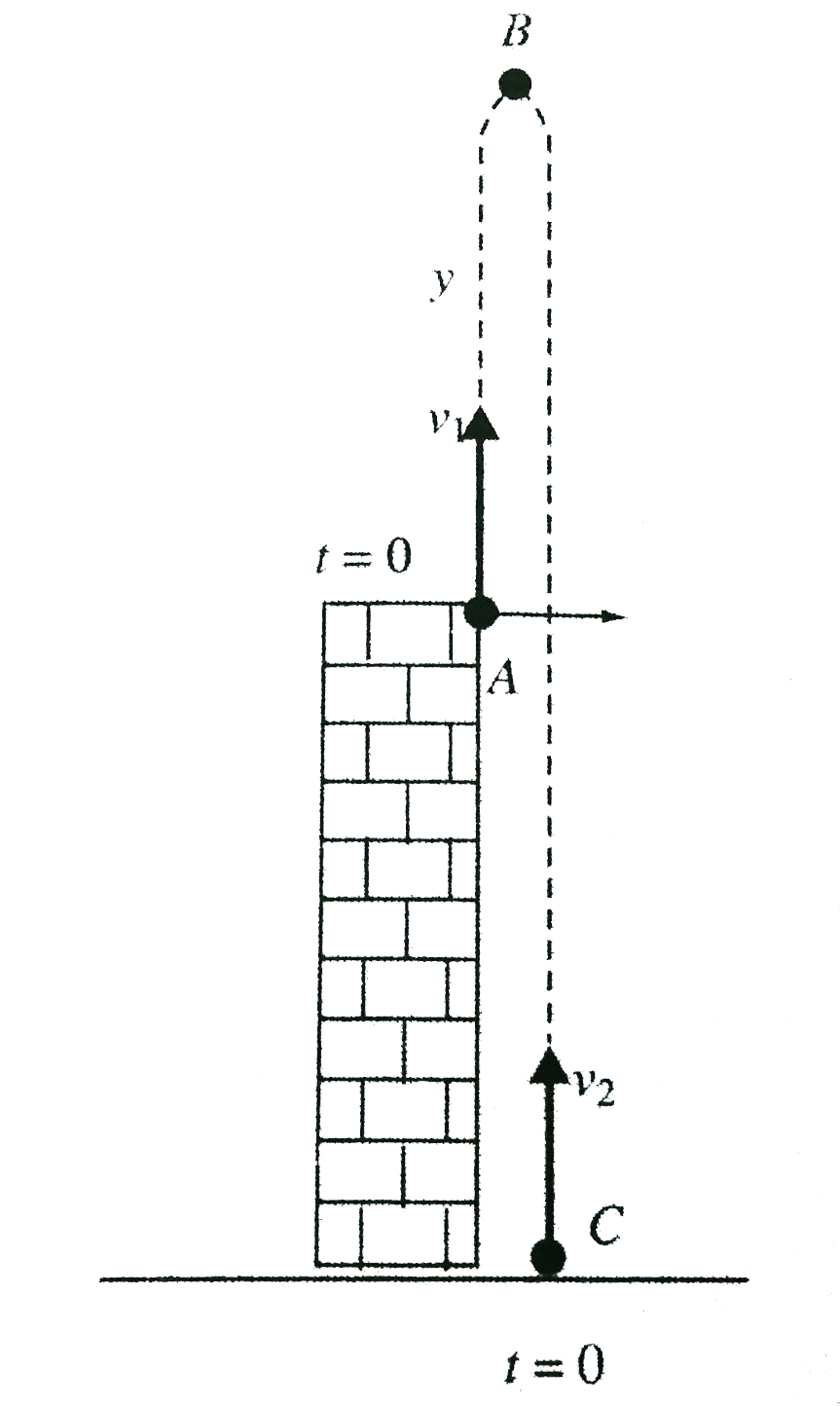 .
.
View SolutionTwo paarticles 1 and 2 are projected simultaneusly with velocities v1 and v2, respectively. Particle 1 is projectected vertically up from the top of a cliff of heitht h and particle 2 is projected vertically up from the bottom of the cliff. If the bodies meet (a) above the top of the cliff, (b) between the top and bottom of the the cliff, and (c ) below the bottom of the cliff, find the time of meeting of the particles.
 .
.
View Solution
