A particle is projected vertically upwards from O with a velocity and a second particle is projected at the same instant from P (at a height h above O) with velocity v at an angle of projection $θ$ with the horizontal. Find the time when the distance between them is minimum. Take $v = 5 m / s$ and $h = 20 m$

Text Solution

Verified by Experts

The correct Answer is:2

In from of ball thrown from p

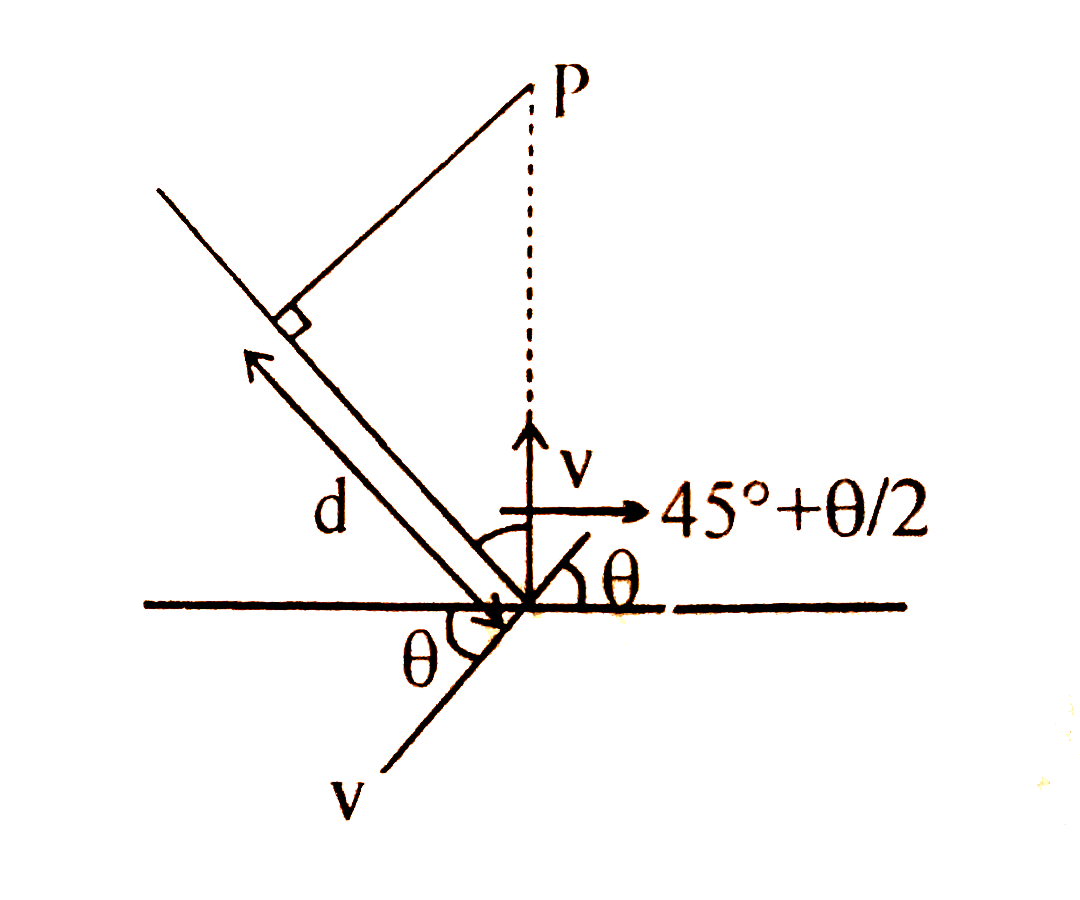
$v_{resultant} = 2 v cos (\frac{90^{\circ} + θ}{2})$
$= 2 v cos (45^{\circ} + θ / 2)$
$t = \frac{d}{v_{resultant}} = \frac{h cos (45^{\circ} + \frac{θ}{2})}{2 v cos (45^{\circ} + \frac{θ}{2})} = \frac{h}{2 v}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle is projected vertically upwards from the ground with a speed V and a speed v and a second particle is projected at the same instant from a height h directly above the first particle with the same speed v at an angle of projection $θ$ with the horizontal in upwards direction. The time when the distance between them is minimum is
A $\frac{h}{2 υ sin θ}$
B $\frac{h}{2 υ cos θ}$
C $h / υ$
D $\frac{h}{2 υ}$
Question 2 - Select One
A particlele is projected vertically upwards from the ground with a speed V and a speed v and a second particle is projected at the same instant from a height h directly above the first particel with the same speed v at an angle of projection $θ$ with the horizontal in upwards direction. The time when the distance between them is minimum is
A $\frac{h}{2 v sin θ}$
B $\frac{h}{2 v cos θ}$
C $\frac{h}{\sqrt{2} v}$
D $\frac{h}{2 v}$
Question 3 - Select One
A particle is projected vertically upwards and it reaches the maximum height H in time T seconds. The height of the particle at any time t will be-
A ${g (t - T)}^{2}$
B $H - \frac{1}{2} {g (t - T)}^{2}$
C $\frac{1}{2} {g (t - T)}^{2}$
D $H - {g (t - T)}^{2}$

BANSAL-TEST PAPERS-PHYSICS PART (C )

Home
Ask Doubt
Profile