A boat going down stream crosses a float at a point A. 't1' minutes later the boat reverses its direction and in the next 't2' minutes it crosses the float at a distance L from the point A. The velocity of the river is
2L/t1
L/(t1+2t2)
2L/(2t1+t2)
L/2t1
The correct Answer is:D
Topper's Solved these Questions
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (A BOAT IN A RIVER)
10 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (OBLIQUE PROJECTION)
62 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (MOTION IN A PLANE)
20 Videos
- RAY OPTICS BOOK - AAKASH SERIESCHAPTER - RAY OPTICS EXERCISE - EXERCISE III
64 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Integer Type Questions
7 Videos
Similar Questions
A float is overcome by a motor boat going downstream at a point A. Thours later it turns back and after some time it passes the float at a distance d km from point A. What is the velocity of stream if the speed of motor remains constant w.r.t. water?
View SolutionA float is overcome by a motor boat going downstream at a point A. Thours later it turns back and after some time it passes the float at a distance d km from point A. What is the velocity of stream if the speed of motor remains constant w.r.t. water?
View Solution
Knowledge Check
A motor boat going down stream comes over a floating body at a point A. 60 minutes later it turned back and after some time passed the floating body at a distance of 12km from the point A.Find the velocity of the stream assuming constant velocity for the motor boat in still water.
A2km/hrB3km/hrC4km/hrD6km/hrA boat takes 4hr upstream and 2hr down the stream for covering the same distance.The ratio of velocity of boat to the water in river is.
A1:3B3:1C1:√3D√3:1A boat which has a speed of 5km per hour in still water crosses a river of width 1 km along the shortest possible path in fifteen minutes. The velocity of the river water in km per hour is :-
A1B2C3D√41
When a boat travels in a river (strictly in a straight line), it can go either in the direction of flow of river (i.e downstream) or in the direction opposite the flow of river (i.e. upstrem ). Thus the boat's actual speed is more than by which it can move in stationary water while travelling downstram (as river's flow speed is added to it) and less while travelling upstream (as the boat moves against the flow of river).Based on the given information answer the following questions A boat going downstream in a following river overcome a raft at a point P. 1 h later it turned back and after some time passed the raft at a distance 6 km from point P.
After reversing its direction ,how much time was taken by the boat to meet the raft again ( i.e. 2nd time) ?
View SolutionTwo persons P and Q crosses the river starting from point A on one side to exactly opposite point B on the other bank of the river. The person P crosses the river in the shortest path. The person Q crosses the river in shortest time and walks back to point B. Velocity of river is 3 kmph and speed of each boat is 5 kmph w.r.t river. If the two persons reach the point B in the same time, then the speed of walk of Q is
View SolutionA boat takes 4 hr upstream and 2 hr down the stream for covering the same distance. The ratio of velocity of boat to the water in river is
View SolutionA boat can be rowed in still water at a speed u. The boat is moving downstream in a river in which water flows at a speed v. There is raft floating in water and therefore moving along with water at speed v. Let the boat overtakes the raft at the moment t = 0.
If the raft has covered a distance x during the interval in which boat overtakes the raft, turns back and crosses it again the speed of stream is
View SolutionA man is boat intends to cross river from A. If he rows perpendicular to the banks then he takes t1 = 10 minutes to reach the other bank and he reaches point C at a distance l = 120 m down the stream from the point B which is exactly opposite to A on the other bank. If he heads at a certain angle α to the straight path AB against the current he will reach point B in t2 = 12.5 minutes.
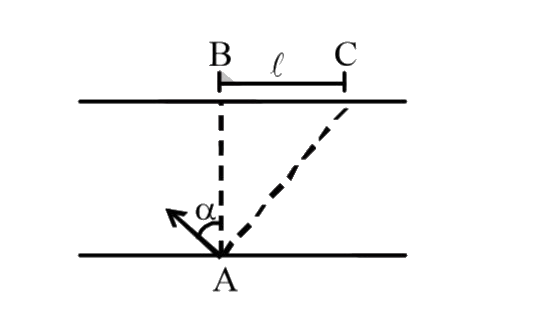
The width of river is-
View Solution
