A spring when compressed by 0.2 m develops a restoring force of 50 N. If a body of mass 10 kg is placed on it, calculate (i) the force constnat (I) of the spring (ii) the depression of the spring (iii) time period of oscillation when the weight is slightly displaced from equilibrium position.
(i) The force constant k=Fx=500.2=250Nm−1
(ii) depression of the spring mgk=10×9.8250=0.392m
(iii) Time period
T=2π√mk=2π√10250=2×3.145=1.2568s
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE I
184 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE II
175 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE-3
49 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
12 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5 Videos
Similar Questions
A spring compressed by 0.2 m develops a restoring force of 25 N. A body of mass 5 kg is placed over it. Deduce (i) force constant of the spring (ii) the depression of the spring under the weight of the body and (iii) the period of oscillation, if the body is disturbed. Take g=10Nkg−1.
View SolutionA spring compressed by 0.1m develips a restoring force 10N. A body of mass 4kg is placed on it. Deduce (i) the force constant of the spring (ii) the depression of the spring under the weight of the body ( take g=10N/kg) and (iii) the period of oscillation, if the body is left free.
View Solution
Knowledge Check
When a spring is compressed by 0.05 m a restoring force of 10 N is developed in it. Then the force constant of the spring is
A50 N/mB100 N/mC150 N/mD200 N/m
On compressing a spring by 0.5 m, a restoring force of 20 N is developed. When a body of mass 5 kg is placed on the spring, then calculate the (a) force constant of the spring.
(b) the distance through which the spring is depressed under the weight of the body.
(c ) the period of oscillation of the spring if the the body is pushed down and then released.
View SolutionA body of mass 2 kg is made to oscillate using a spring of force constant 8Nm−1 find (i) angular frequency (ii) frequency of vibration (iii) time period of vibration.
View SolutionFigure shows a force compression curve of a spring. A body of mass 5kg moving with the velocity of 8m/s hits the spring. Calculate the force constant of the spring and also the compression produced in the spring when the body hits it.
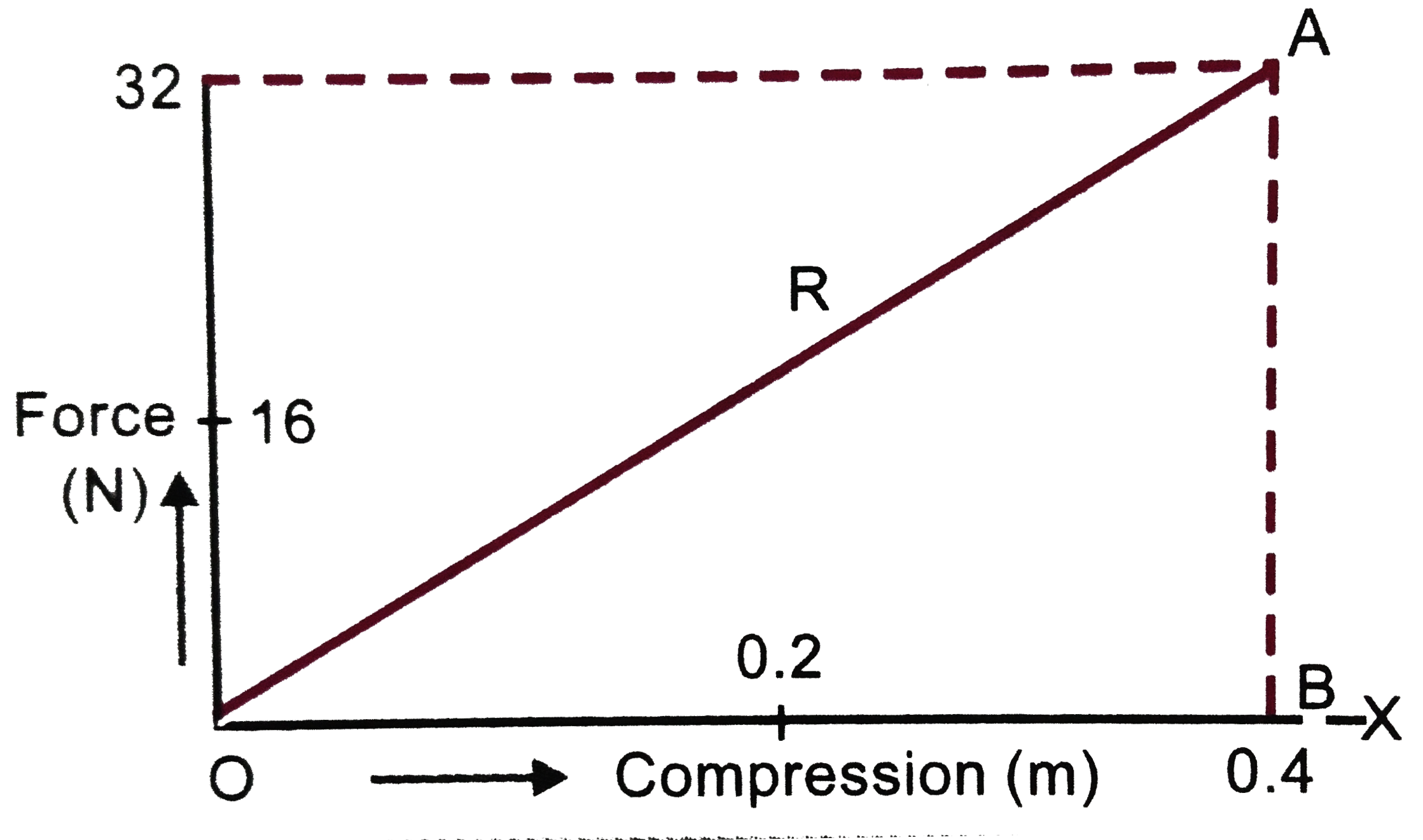
View SolutionThe time period of oscillation of a spring is 1.57s when a mass of 100 gm is suspended from its lower end. Calculate (i) the force constant of the spring (ii) the K.E. of the mass when its displacement'is equal to the amplitude.
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA body of mass 4 kg is made to oscillate on a spring of force constant 10 N/m. Calculate (i) angular frequency (2) frequency of vibration and (3) time period of vibration.
View Solution
