A bar of mass m resting on a smooth horizontal plane starts moving due to the force F=mg/3 of constant magnitude. In the process of its rectilinear motion the angle α between the direction of this force and the horizontal varies as α=as, where a is a constant and s is the distance traversed by the bar from its initial position. Find the velocity of the bar as a function of the angle 'α'
V=√2gsinα3a
Similar Questions
A block of mass m resting on a smooth horizontal plane starts moving due to a constant force F=mg/3 of constant magnitude. In the process of its rectilinear motion the angle θ varies as θ=λs, where λ is constant and s is the distance traversed by the block from its intial position. Find the velocity of the block as a function of the angle θ. Also show that the block will never lose contact with the ground.
View SolutionA small bar starts sliding down an inclined plane forming an angle α with the horizontal. The friction coefficient depends on the distance x covered as k=ax, where a is a constant. Find the distance covered by the bar till it stops, and its maximum velocity over this distance.
View Solution
Knowledge Check
A force F of constant magnitude acts on a block of mass 'm' and t=0,initially along positive x-direction. The direction of force F starts rotating with a constant angular velocity ω in anticlockwise sense. Then the magnitude of velocity of the block as a function of time 't' is ( initial block was at rest )
AFmωsin(ωt2)B2Fmωsin(ωt2)CF2mωsin(ωt2)D2F3mωsin(ωt2)A particle is resting over a smooth horizontal floor AT t = 0, a horizontal force starts acting on it. Magnitude of the force increases with time F = kt, where k is a constant. The two curves are drawn for this particle as shown
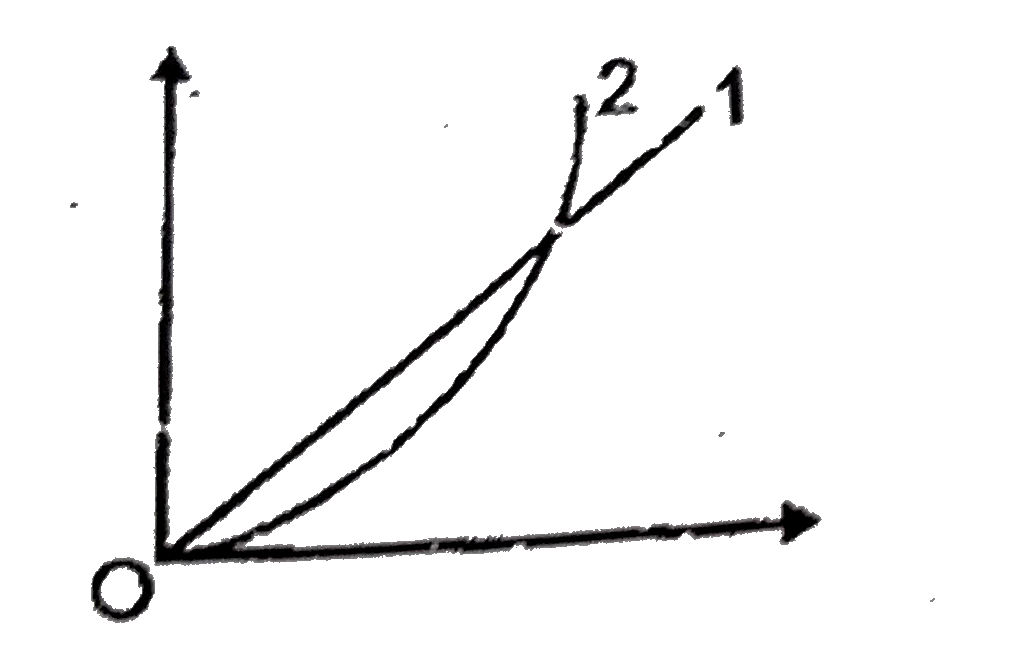 ACurve-1 shows acceleration versus timeBCurve-2 shows velocity versus timeCCurve-2 shows velocity versus accelerationDCurve-1 shows velocity versus acceleration
ACurve-1 shows acceleration versus timeBCurve-2 shows velocity versus timeCCurve-2 shows velocity versus accelerationDCurve-1 shows velocity versus acceleration
A point moves along an arc of a circle of radius R. Its velocity depends on the distance covered s as v=√s, where a is a constant. Find the angle α between the vector of the total acceleration and the vector of velocity as a function of s.
View SolutionA body of mass m rests on a horizontal plane with the friction coefficient k. At the moment t=0 a horizontal force is applied to it, which varies with time as F=at, where a is a constant vector.
Find the distance traversed by the body during the first t seconds after the force action began.
View SolutionA locomotive of mass m starts moving so that its velocity varies according to the law V=α√s, where α is a constant and s is the distance covered. Find the total work done by all the forces acting on the locomotive during the first t seconds after the beginning of motion.
View SolutionA locomotive of mass 'm' starts moving so that its velocity varies as v=αs23 where α is a positive constant and 's' is the distance travelled .The total work done by all the forces acting on the locomotive during first 't' second after the start of motion is
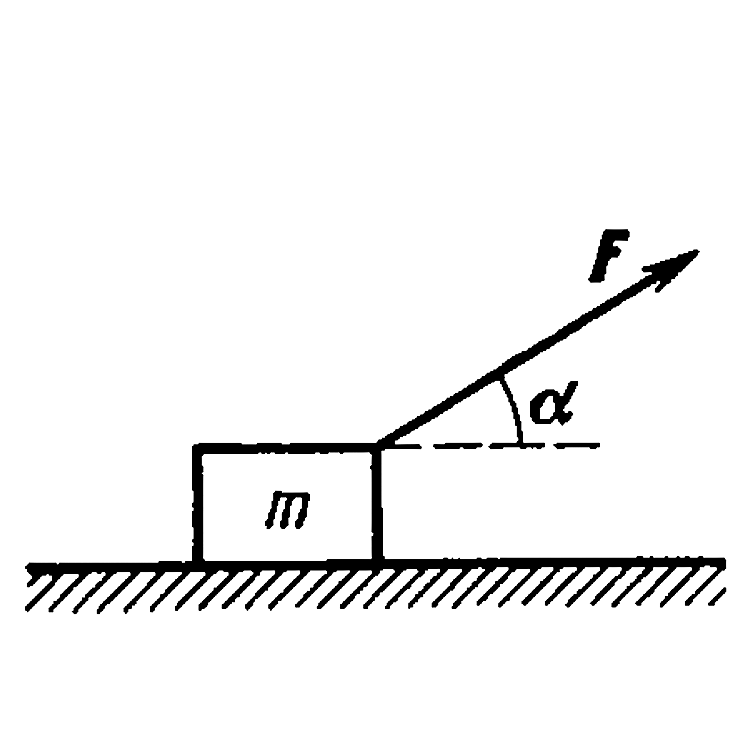
View SolutionAt the moment t=0 the force F=at is applied to a small body of mass m resting on a smooth horizontal plane (a is constant).
The permanent direction of this force forms an angle α with the horizontal (figure). Find:
(a) the velocity of the body at the moment of its breaking off the plane,
(b) the distance traversed by the body up to this moment.
View SolutionA force F of constant magnitude acts on a block of mass 'm' and t=0,initially along positive x-direction. The direction of force F starts rotating with a constant angular velocity ω in anticlockwise sense. Then the magnitude of velocity of the block as a function of time 't' is ( initial block was at rest )
View Solution
