At the moment t=0 the force F=at is applied to a small body of mass m resting on a smooth horizontal plane (a is constant).
The permanent direction of this force forms an angle α with the horizontal (figure). Find:
(a) the velocity of the body at the moment of its breaking off the plane,
(b) the distance traversed by the body up to this moment.
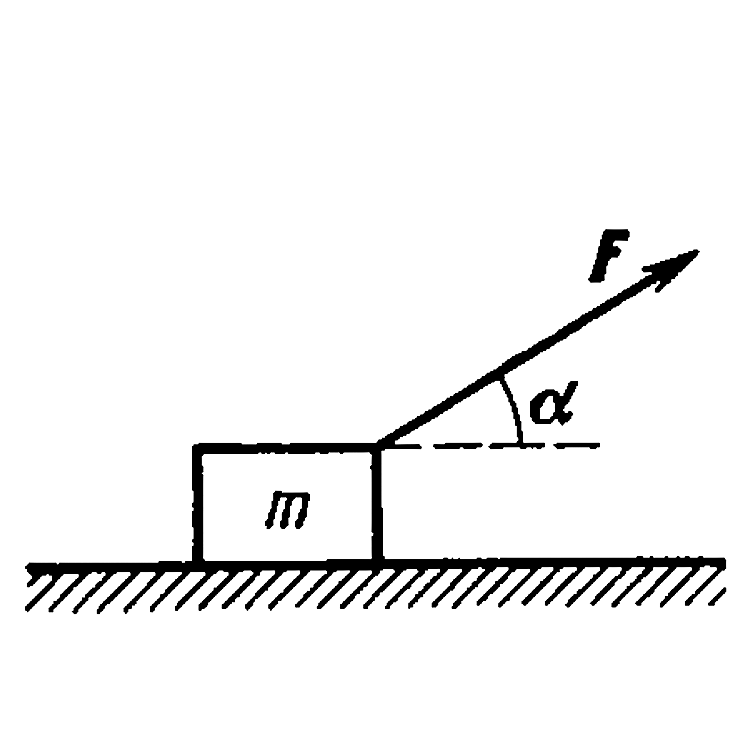
First of all let us draw the free body diagram for the small body of mass m and indicate x-axis along the horizontal plane and y-axis, perpendicular to it, as shown in the figure.
Let the block breaks off the plane at t=t0 i.e. N=0
So, N=mg−at0sinα=0
or, t0=mgasinα (1)
From Fx=mwx, for the body under investigation:
mdv/dt=atcosα, Integrating within the
limits for v(t)
mv∫0dvx=acosα∫0tdt (using Eq. 1)
So, v=dsdt=acosα2mt2 (2)
Integrating, Eqs. (2) for s(t)
s=acosα2mt33 (3)
Using the value of t=t0 from Eq. (1), into Eqs. (2) and (3)
v=mg2cosα2asin2α and s=m2g3cosα6a2sin3α

Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Laws Of Conservation Of Energy, Momentum And Angular Momentum82videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation34videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics49videos
PHYSICAL FUNDAMENTALS OF MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena38videos
THERMODYNAMICS AND MOLECULAR PHYSICS
Similar Questions
At t=0, a force F = kt is applied on a block of mass m making an angle α with the horizontal . Suppose surfaces to be smooth. Find the velocity of the body at the time of breaking off the plane.
 View Solution
View SolutionAt the instant t=0, a force F=kt (k is a constant) acts on a small body of mass m resting on a smooth horizontal surface. The time, when the body leaves the surface is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
At the moment t=0 force F=kt is applied to a small body of mass m resting on a smooth horizontal plane (k is a constant) The direction of this force always forms an angle θ with the horizontal as shown.
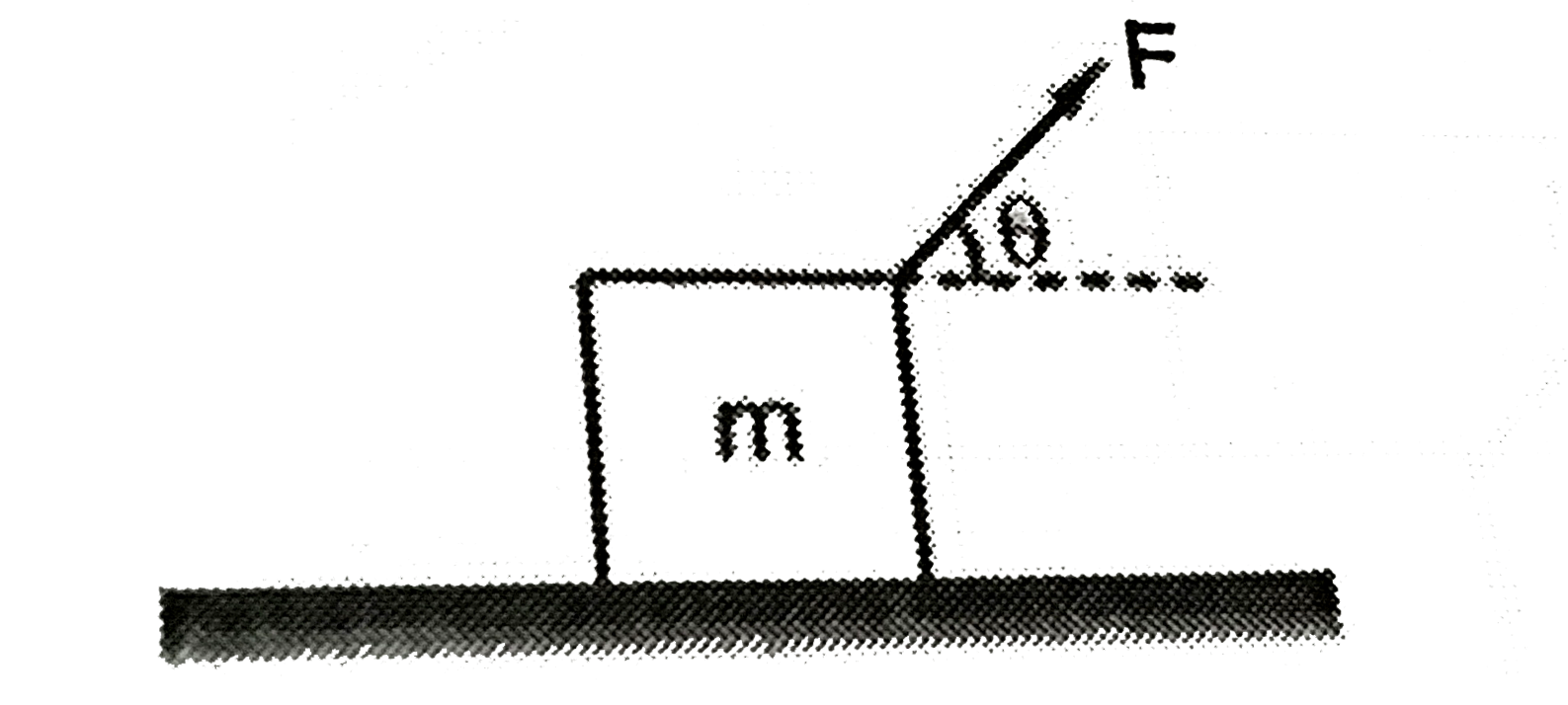
Find the time t at which moment, the body breaks off the plane:Amg2ksinθBmgksinθCmgksin2θD2mgksinθ - Question 2 - Select One or More
At t=0, a force F=at2 is applied to s small body of mass m at an angle α resting on a smooth horizontal plane.
 AVelocity of the body at the moment it breaks off the plane is √mg39atan2αsinαBThe distance travelled by the body before breaking off the plane is mg212asinαtanαCIts acceleration at the time of breaking off the plane is gcotα.DTime at which it breaks off the plane is √mgasinα
AVelocity of the body at the moment it breaks off the plane is √mg39atan2αsinαBThe distance travelled by the body before breaking off the plane is mg212asinαtanαCIts acceleration at the time of breaking off the plane is gcotα.DTime at which it breaks off the plane is √mgasinα - Question 3 - Select One
Work done by the gravitational force on a body of mass ''m'' moving on a smooth horizontal surface through a distance 's' is
AmgsB−mgsC0D2mgs
A constant force of 20N is applied to pull a body of mass 10 k, kept on a smooth horizontal surface. What is the increase in its kinetic energy if the body starts from rest and covers a distance of 5m?
View SolutionA force of 20N is applied on a body of mass 5 kg resting on a horizontal plane. The body gains a kinetic energy of 10 after is moves a distance 2m. The fricitional force is
View SolutionIf F is the force applied , then acceleration of the body of mass M when body is on rough horizontal surface
View SolutionA horizontal force F is applied on a riing of mass m1 constrained to move on a horizontal smooth wire the hanging mass m2 is constant angle with
 View Solution
View SolutionA block is resting over a smooth horizontal plane. A constant horizontal force starts acting on it at t=0. Which of the following graph is correct:
View Solution

