A solid sphere of radius R is projected on a rough horizontal surface of coefficient of friction with linear Speed v0, at time to 0. It slips for some time, finally starts to roll with out slipping at time t=t0 .Find a) The linear velocity of its centre when pure rolling begins. b) The time t0

a) The kinematics equations for the motion of the sphere at time t are
v=v0-at ,where a =μg
ω=αt,where α=μmgR25mR2=5a2R,when pure rolling begins v∣=ω∣R (at t=t0)
V∣=V0−at0(v∣R=5a2Rt0)⎫⎪
⎪
⎪⎬⎪
⎪
⎪⎭⇒7V∣5=V0 or V∣=5V07⇒ Required linear velocity =V∣=5V07
b)v∣=v0μ>0⇒μ>0=v0−v∣=2v07⇒t0=2v07μg
Aliter: The angular momentum of the sphere about the horizontal surface is conserved.
⇒Linitial(at t=t0)
⇒Mv0R=mv∣R+25mR2ωI=mvIR2×vIR=75mvIR⇒VI=57v0
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Very short answer type questions
40 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Numerical Exercise (LEVEL-1)
18 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Integer Type Questions
7 Videos
- SIMPLE HARMONIC MOTION BOOK - AAKASH SERIESCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II)(PRACTICE SHEET (ADVANCED)) (INTEGER TYPE QUESTIONS)
3 Videos
Similar Questions

A solid sphere of mass ma nd radis R is placed on a rough horizontal surface A horizontal force F is applied to sphere at a height h, (0≤h≤R) from centre. If sphere rolls slipping then,
View SolutionA ring of mass m and radius R is placed on a rough horizontal surface (co-efficient of friction μ) with velocity of C.M.v0 and angular speed 2V0R as shown in figure. Initially the ring is rolling with slipping but attains pure rolling motion after some time t. Then
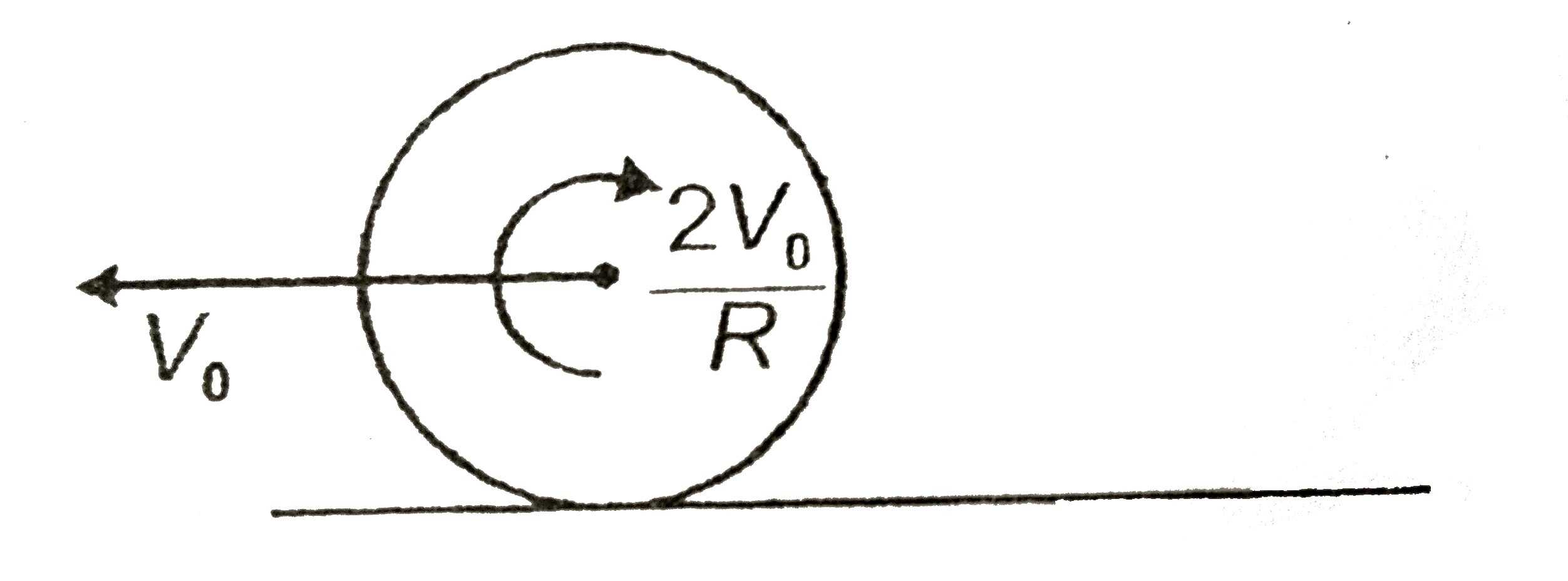
View Solution
Knowledge Check

A solid sphere of mass ma nd radis R is placed on a rough horizontal surface A horizontal force F is applied to sphere at a height h, (0≤h≤R) from centre. If sphere rolls slipping then,AThe maximum possible acceleration of sphere is FMBThe maximum possible acceleration of sphere is 10F7MCThe magnitude of friction force acting on the sphere is zero if h=2R5DThe magnitude of friction force acting on the sphere is zero h=3R4.
A solid sphere is rolling purely on a rough horizontal surface (coefficient of kinetic friction =μ) with speed of centre =u. It collides in-elastically with a smooth vertical wall at a certain moment, the coefficient of restituting being 12. The sphere will begin pure rolling after a time.A3u7μgB2u7μgC3u5μgD2u5μg
A ring of mass m and radius R is placed on a rough horizontal surface (co-efficient of friction μ) with velocity of C.M.v0 and angular speed 2V0R as shown in figure. Initially the ring is rolling with slipping but attains pure rolling motion after some time t. Then
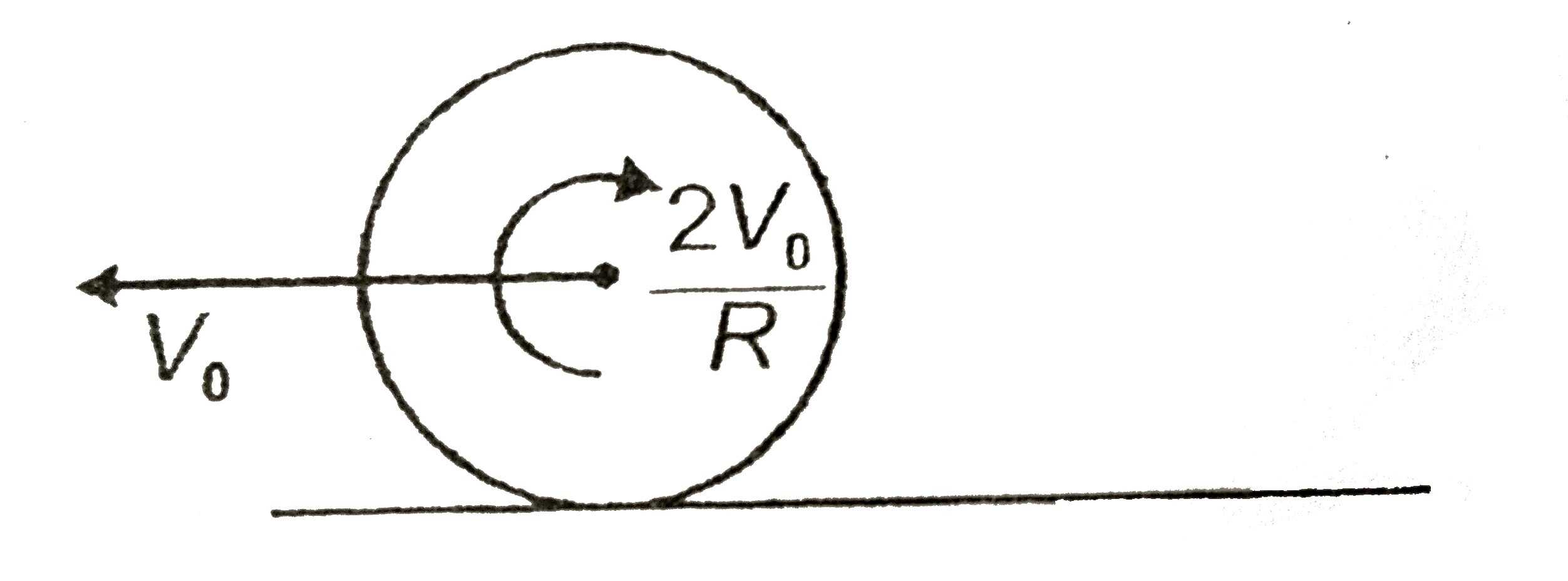
View SolutionA sphereicla ball of mass M and radius R is projected along a rough horizontal surface so that initially (t=0) it slides with a linear speed v0 but does not rotate. As it slides, it begins to spin and eventually rolls without slipping. How long does it take to begin rolling without slipping?
View Solution
A solid sphere is rolling purely on a rough horizontal surface (coefficient of kinetic friction =μ) with speed of centre =u. It collides inelastically with a smooth vertical wall at a certain moment, the coefficient of restituting being 12. The sphere will begin pure rolling after a time.
View Solution
solid sphere of radius r is gently placed on a rough horizontal ground with an initial angular speed ω0 and no linear velocity. If the coefficient of friction is μ, find the time t when the slipping stops. in addition state the linear velocity v and angular velocity ω at the end of slipping
View Solution
solid sphere of radius r is gently placed on a rough horizontal ground with an initial angular speed ω0 and no linear velocity. If the coefficient of friction is μ, find the time t when the slipping stops. in addition state the linear velocity v and angular velocity ω at the end of slipping
View Solution(i) A solid sphere of radius R is released on a rough horizontal surface with its top point having thrice the velocity of its bottom point A (VA=V0) as shown in figure. Calculate the linear velocity of the centre of the sphere when it starts pure rolling.
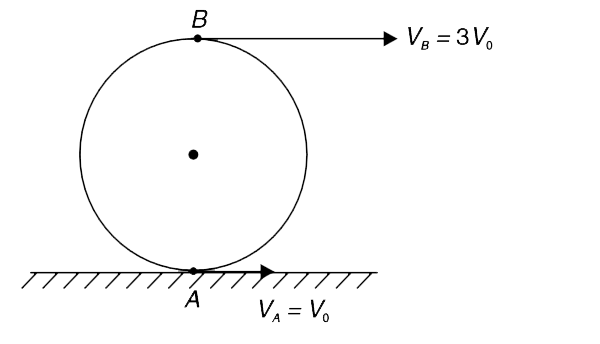
(ii) Solid sphere of radius R is placed on a rough horizontal surface with its centre having velocity V0 towards right and its angular velocity being ω0 (in anticlockwise sense). Find the required relationship between V0 and ω0 so that -
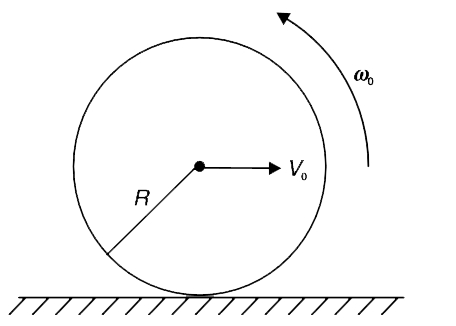
(a) the slipping ceases before the sphere loses all its linear momentum.
(b) the sphere comes to a permanent rest after some time.
(c) the velocity of centre becomes zero before the spinning ceases.
View Solution
