solid sphere of radius r is gently placed on a rough horizontal ground with an initial angular speed ω0 and no linear velocity. If the coefficient of friction is μ, find the time t when the slipping stops. in addition state the linear velocity v and angular velocity ω at the end of slipping
 ltbr Let m be the mass of the sphere
ltbr Let m be the mass of the sphere
since, it is a case of backward slipping, force of friction is in forward direction limiting friction will act in this case
linear acceleration a=fm=μmgm=μg
angular retardation α=τI=f.r25mr2=52μgr
slipping is ceased when v=rω
or (at)=r(ω0−αt)
or μgt=r(ω0−52μgtr) or 72μgt=rω0
∴t=27rω0μg
v=at=μgt=27rω0
and ω=vr=27ω0
Alternate solution
Net torque on the sphere about the bottommost point is zero as friction is passing through that point therefore, angular mometum of the sphere will remain conserved about the bottommost point
Li=Lf
therforeIω0=Iω+mrv
or 25mr2ω0=25mr2ω+mr(ωr)
∴ω=27ω0 and v=rω=27rω0
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example
1 Video
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.

View SolutionA disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View Solution
Knowledge Check
The correct relation between linear velocity →v and angular velocity →ω of a particle is
A→v=→r×→ωB→v=→ω×→rC→ω=→r×→vD→ω=→v×→rA ring of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is μk. The time after it starts rolling is.
AωoμkR2gBωog2μkRC2ωoRμkgDωoR2μkg
A solid sphere is projected along an inclined plane according to diagram. If coefficient of friction is μ=0.5 and radius R, then find
(a) Time when linear velocity becomes zero
(b) Angular velocity at that instant

View Solution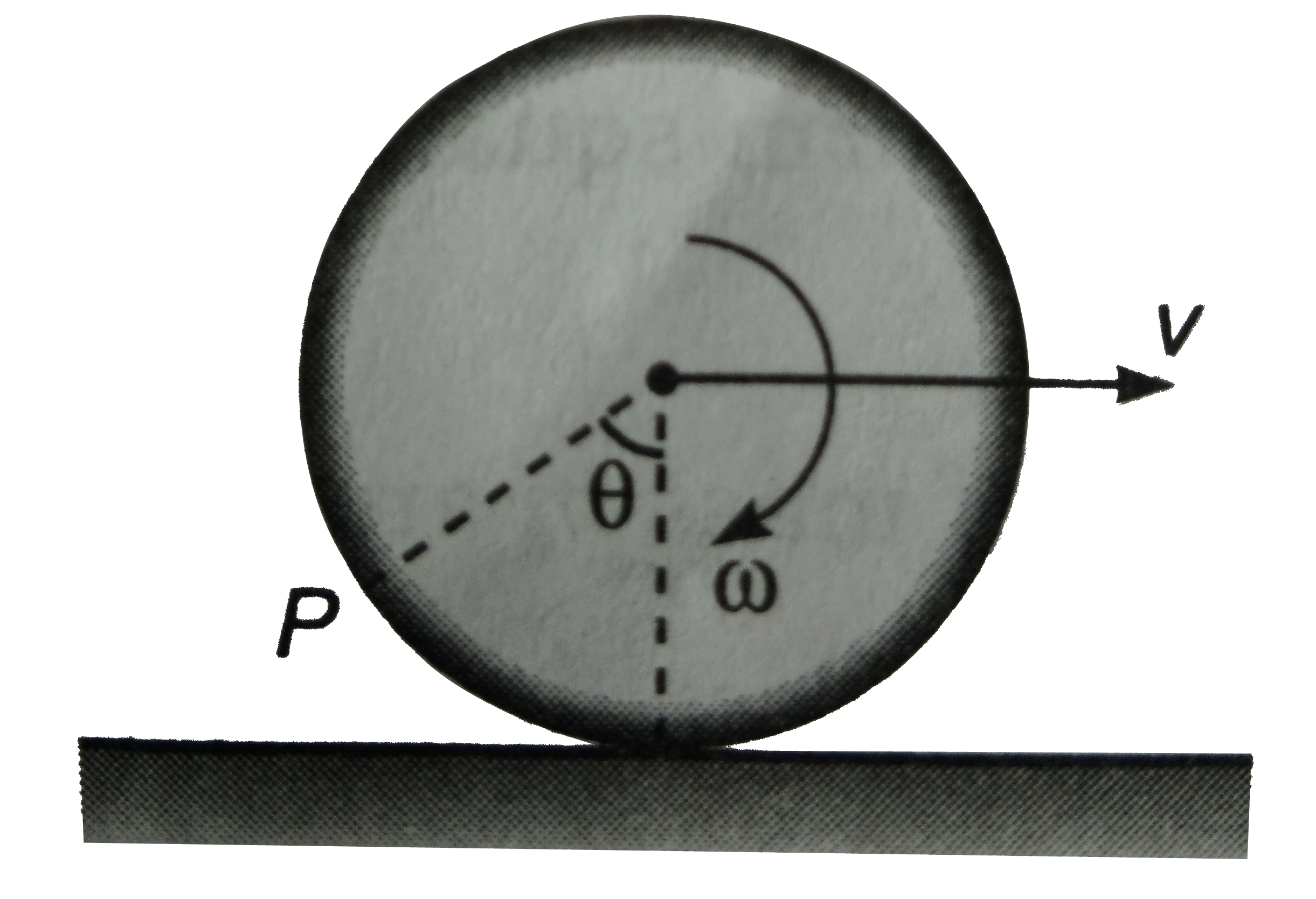
A ring of radius R rolls on a horizontal ground with linear speed v and angular speed ω. For what value of θ the velocity of point P is in vertical direction (v<Rω).
View SolutionChoose the correct option:
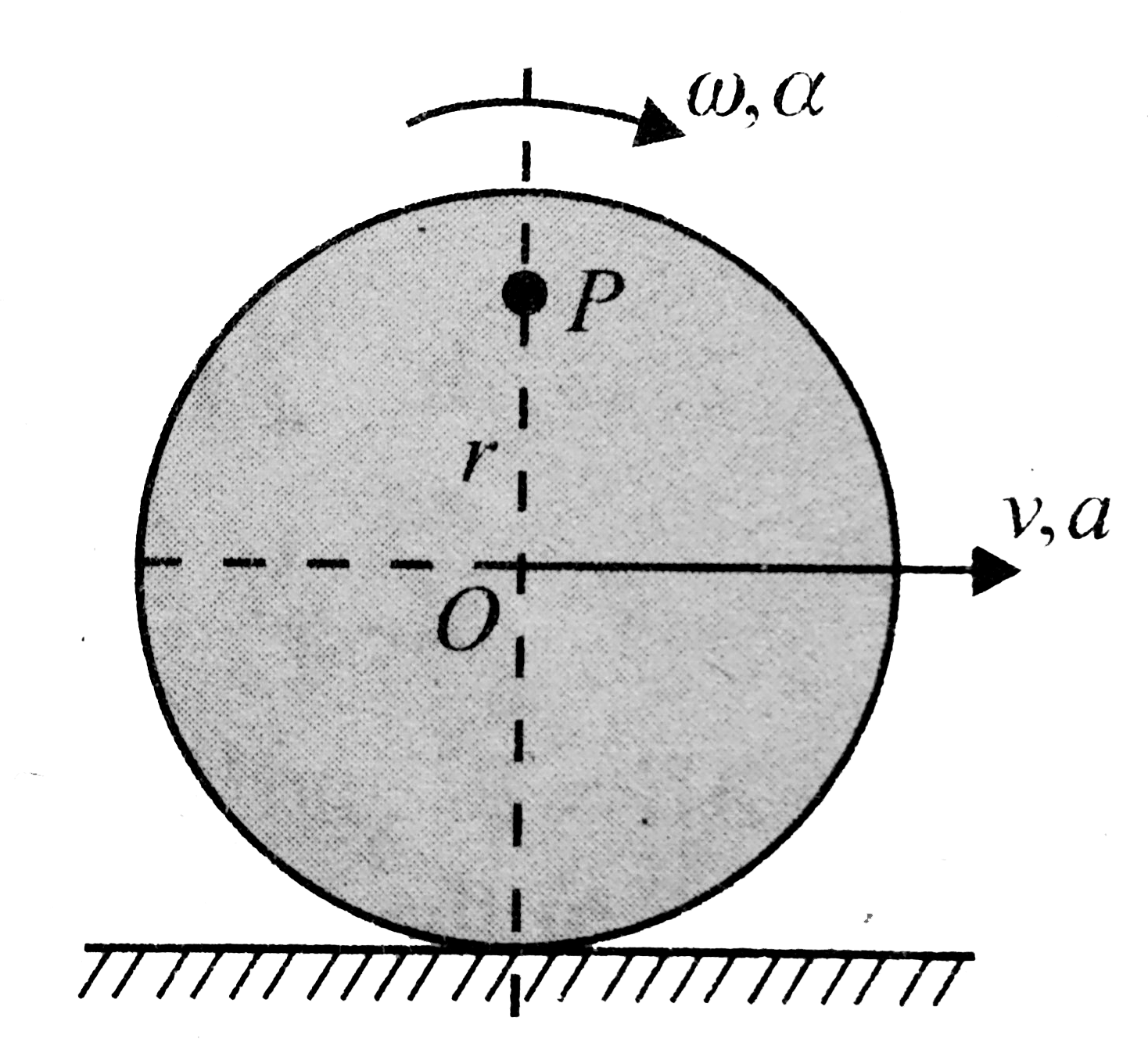
A disc of radius R rolls on a horizontal ground with linear acceleration a and angular acceleration α as shown in Fig. The magnitude of acceleration of point P as shown in the figure at an instant when its linear velocity is v and angular velocity is ω will be a
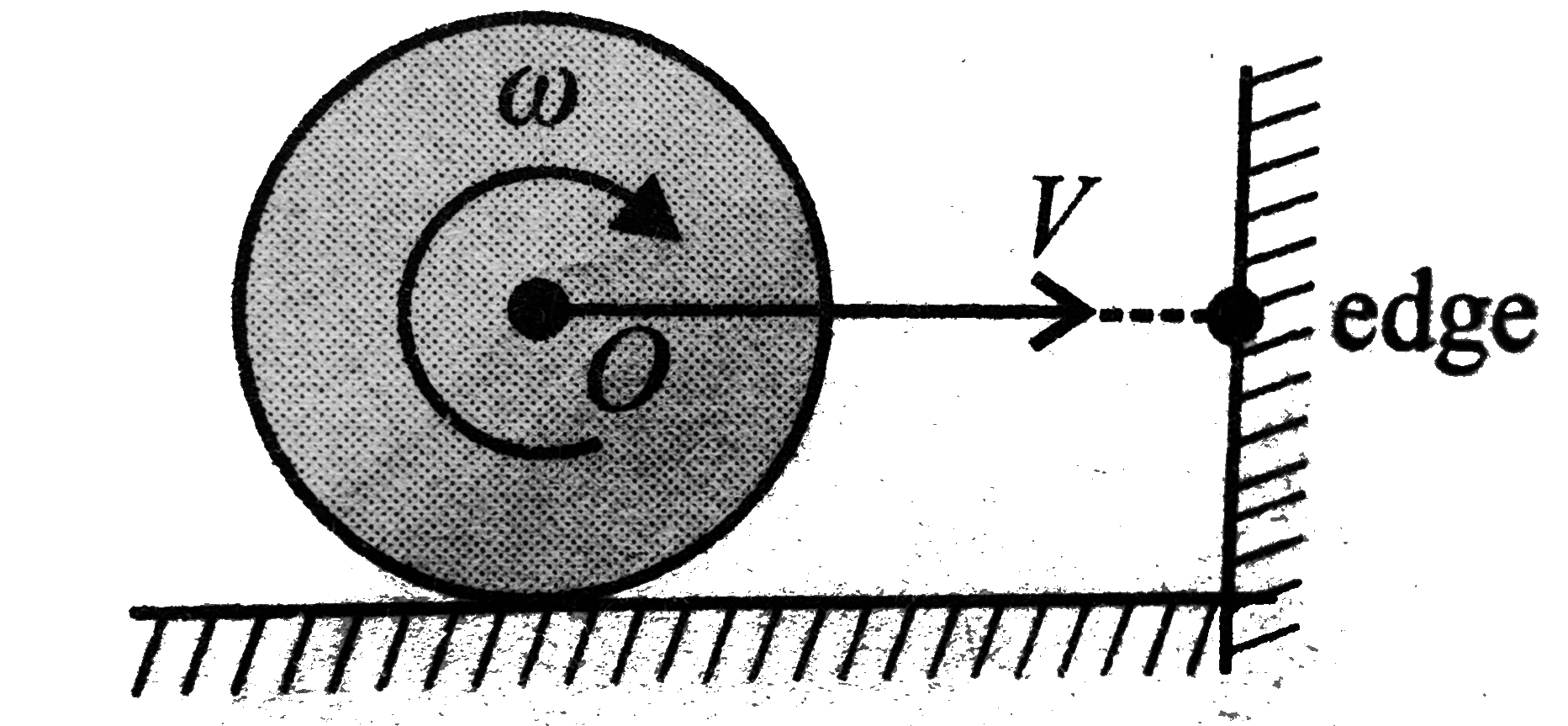
View SolutionA uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity V and angular velocity ω(V=ωr). The sphere collides with a sharp edge on the wall as shown in Fig. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the sphere just after the collision is equal to
View SolutionA uniform sphere of radius R is palced on a rough horizontal surface and given a linear velocity v0 and an angular velocity ω0 as shown . If the angular velocity and the linear velocity both become zero simultaneously, then
View SolutionA disc of radius R rolls on a horizontal ground with linear acceleration a and angular acceleration α as shown in figure. The magnitude of acceleration of point P at an instant when its linear velocity is v and angular velocity is ω will be:

View Solution
