A semicircular ring of mass m and radius R is freely pivoted at O. Find the: i) e of the ring ii) reaction force at O, when the ring is released with an angular speed at the given position. 
α=4g29R,Ny=85mg87.Nx=0
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers20videos
ROTATIONAL MECHANICS
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Numerical Exercise (LEVEL-1)18videos
ROTATIONAL MECHANICS
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Integer Type Questions7videos
ROTATIONAL DYNAMICS
- BOOK - AAKASH SERIESCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II)(PRACTICE SHEET (ADVANCED)) (INTEGER TYPE QUESTIONS)3videos
SIMPLE HARMONIC MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
There is a ring or mass m and radius R is pivoted at a point O on its periphery. It is free to rotate about an axis perpendicular to its plane. What is the period of ring?
AT=2π((Rg))BT=2π√(2Rg)CT=π√(2Rg)DT=2π√(3Rg) - Question 2 - Select One
A thin circular ring of mass per unit length p and radius r is rotating at an angular speed ω as shown in figure. The tension in the ring is
Apω2r2/2Bpω2r2Cpω2r2/3DNone - Question 3 - Select One
A ring of mass m and radius R is rolling on a horizontal plane. If the ring suddenly starts rotating about its diameter, then its angular velocity in this will be
AVRB2VRCV2RD√2VR
A particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionFigure 10-82 is an overhead view of semicircular ring of mass m and radius R that lies on a frictionless surface. The ring is connected by elevated spokes (not shown) to a pivot at the center of the semicircle. The ring can rotate around that pivot but is initially stationary. A bead of mass m and speed v is shot into the ring, entering under the spokes and tangentially to the ring and then sliding along the ring. The ring and bead then rotate together around the pivot. Find their angular speed.
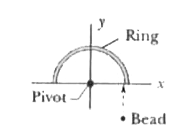
View SolutionA small bead of mass m moving with velocity v gets threaded on a stationary semicircular ring of mass m and radius R kept on a horizontal table. The ring can freely rotate about its centre. The bead comes to rest relative to the ring. What will be the final angular velocity of the system?
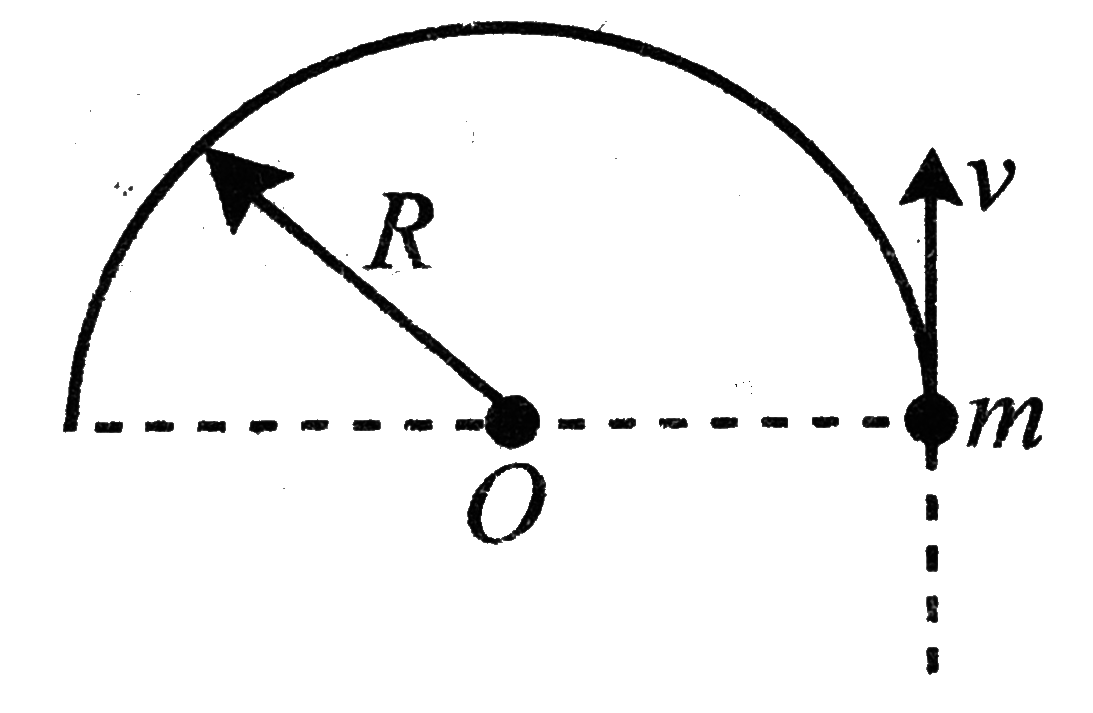
View SolutionA small bead of mass m moving with velocity v gets threaded on a stationary semicircular ring of mass m and radius R kept on a horizontal table. The ring can freely rotate about its centre. The bead comes to rest relative to the ring. What will be the final angular velocity of the system?
View Solution