Find the time taken for height of water level to fall from 'h' to 'h'in a vessel, if water comes out from a small hole at the bottom
From equation of continity for an incompressible liquid Av1=a√2gh (or) v1=(aA)√2gh
where v1 is the rate of descendence of the level of free surface. So, v1 can be written as: V1=−dhdt
∴−dhdt=(aA)√2gh (or) h1∫hdh√h=−(aA)√2gt∫t=0dt
∴2(√h1−√h)=−(aA)(√2g)t (or)t=2Aa√2g(√h1−√h)∝t
Topper's Solved these Questions
- FLUID MECHANICSBOOK - AAKASH SERIESCHAPTER - FLUID MECHANICSEXERCISE - Test your self
6 Videos
- FLUID MECHANICSBOOK - AAKASH SERIESCHAPTER - FLUID MECHANICSEXERCISE - Short answer type questions
13 Videos
- FLUID MECHANICSBOOK - AAKASH SERIESCHAPTER - FLUID MECHANICSEXERCISE - ADDITIONAL PRACTICE SHEET (ADVANCED) (Straight Objective Type Questions)
5 Videos
- EXPANSION OF SOLIDS BOOK - AAKASH SERIESCHAPTER - EXPANSION OF SOLIDS EXERCISE - Questions for Descriptive Answers
5 Videos
- FRICTION BOOK - AAKASH SERIESCHAPTER - FRICTION EXERCISE - ADDITIONAL PRACTICE EXERCISE PRACTICE SHEET (ADVANCED) (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
1 Videos
Similar Questions
A vessel whose bottom has round holes with a diameter of d=0.1mm is filled with water. The maximum height of the water level h at which the water does not flow out, will be (The water does not wet the bottom of the vessel). [STofwater=70dyne/cm]
View SolutionA cylindrical vessel filled with water to a hight H. A vessel has two small holes in the side, from which water iins rushing out horizontal and the two steams stike the ground at the same poin, if the lower hole Q Q is h height above the ground, then the height of hole P above the ground will be
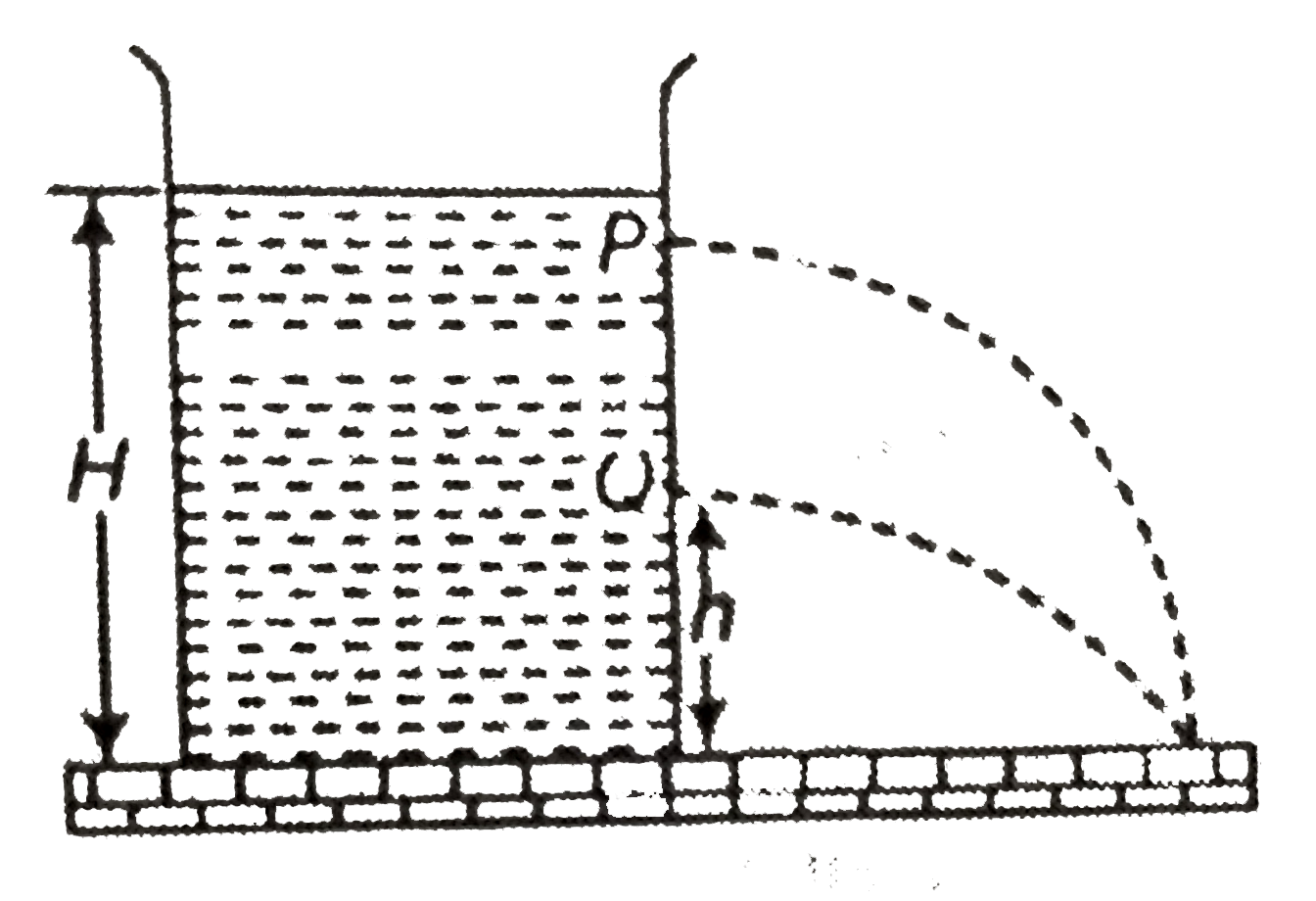
View Solution
Knowledge Check
A vessel whose bottom has round holes with a diameter of d=0.1mm is filled with water. The maximum height of the water level h at which the water does not flow out, will be (The water does not wet the bottom of the vessel). [STofwater=70dyne/cm]
Ah=24.0cmBh=25.0cmCh=26.0cmDh=28.0cmA tube is attached as shown in closed vessel containing water. The velocity of water coming out from a small hole is :
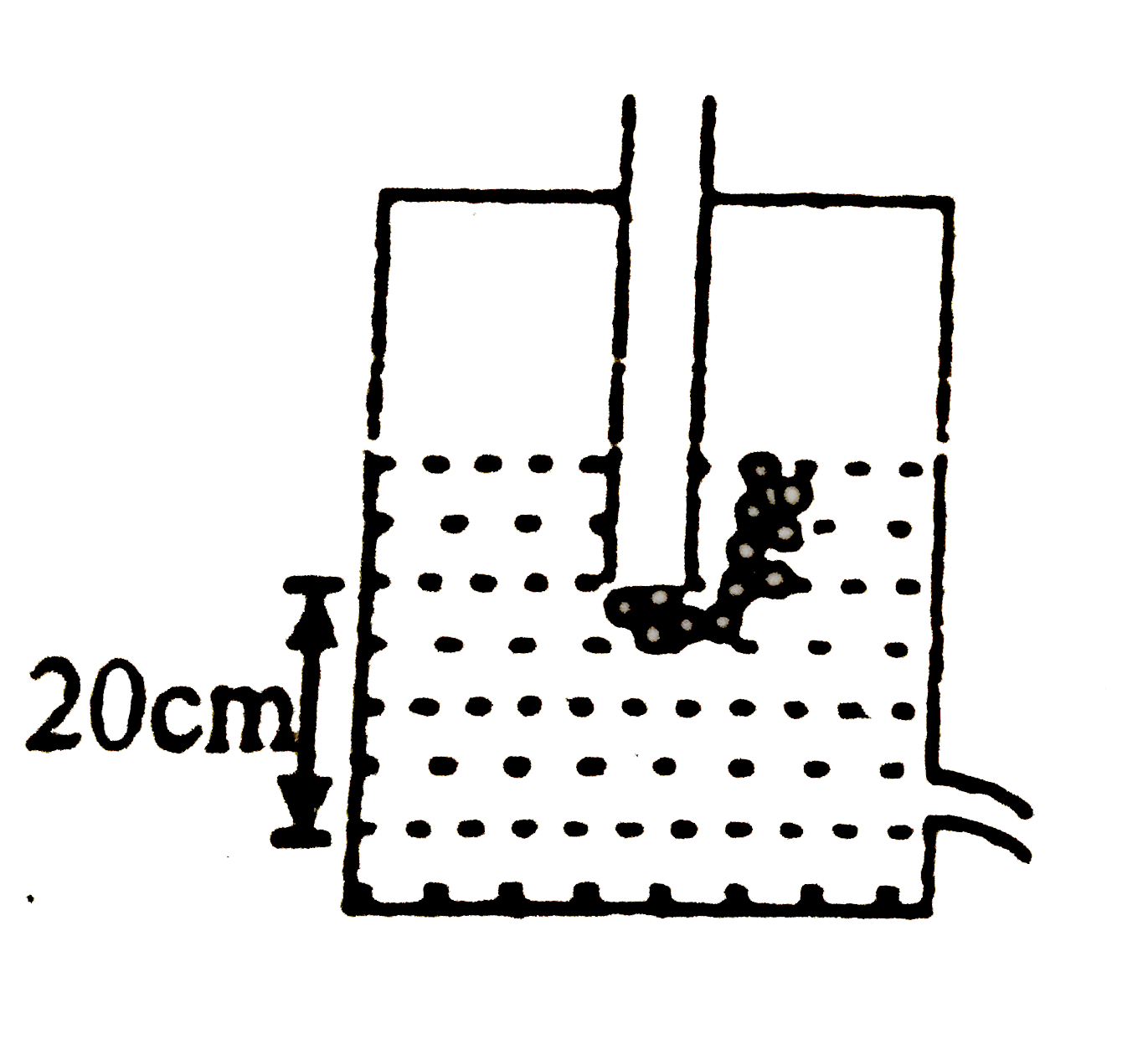 A√2m/sB2m/sCdepends on pressure of air inside vesselDNone of these
A√2m/sB2m/sCdepends on pressure of air inside vesselDNone of theseA large tank filled with water to a height h is to be emptied through a small hole at the bottom. The ratio of times taken for the level of water to fall from h to h2 and from h2 to zero is
A√2B12C√2−1D1√2−1
A cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionShows a large closed cylindrical tank containing water, Initially the air trapped above the water surface has a height h0and pressure2p0where p0is the atmospheric pressure. There is a hole in the wall of tank at a depth h1below the top from which water comes out. A long vertical tube is connected as shown. (a) Find the height h2 of the water in the long tube above the top initially. (b) Find the speed with which water comes out of hole.(c)Find the height of the water in the long tube above the top when the water stops coming out of the hole.

View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View Solution
