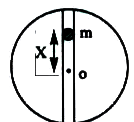
A tunnel is dug along the diameter of the earth. The gravitational force on particle of mass m placed in the tunnel at a distance 'x' from the centre.

Text Solution

Verified by Experts

Mass of earth $M = \frac{4}{3} π R^{3} ρ$
Mass of imaginary sphere, having radius x,
$M^{1} = \frac{4}{3} π x^{3} ρ$ (or) $\frac{M^{1}}{M} = \frac{x^{3}}{R^{3}}$
$∴$ gravitational force on .m. due to $M_{1}$
$F = \frac{G M^{1} m}{x^{2}}$ (or)
$F = \frac{G m}{x^{2}} (\frac{x^{3}}{R^{3}} M) = \frac{G M m x}{R^{3}}$

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Assume that a tunnel is dug through earth from North pole to south pole and that the earth is a non-rotating, uniform sphere of density $ρ$ . The gravitational force on a particle of mass m dropped into the tunnel when it reaches a distance r from the centre of earth is
A $(\frac{3}{4 π} m G ρ) r$
B $(\frac{4 π}{3} m G ρ) r$
C $(\frac{4 π}{3} m G ρ) r^{2}$
D $(\frac{4 π}{3} m^{2} G ρ) r$
Question 2 - Select One
If a tunnel is dug along the diameter of the earth and a ball is dropped into the tunnel, it will have
Alinear motion
Bcircular motion
Coscillatory motion
Dtranslatory motion

AAKASH SERIES-GRAVITATIONAL-EXERCISE -3

Home
Ask Doubt
Profile