It is possible to project a particle with a given speed in two possible ways so that it has the same horizontal range 'R'. The product of time taken by it in the two possible ways is
R/g
2R/g
3R/g
4R/g
The correct Answer is:B
Topper's Solved these Questions
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (HORIZONTAL PROJECTILE MOTION)
28 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (CIRCULAR MOTION)
2 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (A BOAT IN A RIVER)
10 Videos
- RAY OPTICS BOOK - AAKASH SERIESCHAPTER - RAY OPTICS EXERCISE - EXERCISE III
64 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Integer Type Questions
7 Videos
Similar Questions
A particle is projected with certain velocity at two different angles of projections with respect to horizontal plane so as to have the same range 'R' ona horizontal plane. If't1' and 't2' are the times taken for the two paths, then which one of the following relations is correct?
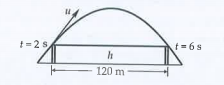
View SolutionAn object projected with same speed at two different angles covers the same horizontal range R. If the two times of flight be t1andt2 . The range is 1αgt1t2, the value of α is
View Solution
Knowledge Check
It is possible to project a particle with a given velocity in two possible ways so as to make it pass through a point at a distance r from the point of projection. The product of times taken to reach this point in the two possible ways is then proportional to
ArBr2C1/rD1/r2A projectile is projected with a kinetic energy K. If it has the maximum possible horizontal range, then its kinetic energy at the highest point will be
AK/4BK/2C3K/4DKA particle is projected at angle θ from horizontal. The product of the two possible times it take to pass over the height h(h<Hmax) is
A2ugB2hgC2usinθgDNone
An object projected with same speed at two different angles covers the same horizontal range R. If the two times of flight be t1andt2 . The range is 1αgt1t2, the value of α is
View SolutionTwo particles are projected with same velocity but at angles of projection 35 and 55 then their horizontal ranges are in the ratio of
View SolutionIs it possible for the same
angle to have two different measures ?
View SolutionThere are two angles of projection for which the horizontal range is the same. Show that the sum of the maximum heights for these two angles is independent of the angle of projection.
View Solutiontwo particles are projected upwards with the same initial velocity v0 in two different angles of projection such that their horizontal ranges are the same. The ratio of the heights of their horizontal ranges are the same. The ratio of the heights of their highest point will be
View Solution
