A particle is projected from the ground with velocity u making an angle θ with the horizontal. At half of its maximum heights,
its horizontal velocity is ucosθ
its vertical velocity is usinθ√2
its velocity is u(1+cos2θ2)12
all the above are true
The correct Answer is:D
Topper's Solved these Questions
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (HORIZONTAL PROJECTILE MOTION)
28 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (CIRCULAR MOTION)
2 Videos
- RIVISION EXERCISEBOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - MOTION IN A PLANE (A BOAT IN A RIVER)
10 Videos
- RAY OPTICS BOOK - AAKASH SERIESCHAPTER - RAY OPTICS EXERCISE - EXERCISE III
64 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Integer Type Questions
7 Videos
Similar Questions
A body is projected from ground with velocity u making an angle θ with horizontal. Horizontal range of body is four time to maximum height attained by body. Find out
(i) angle of projection
(ii) Range and maximum height in terms of u
(iii) ratio of kinetic energy to potential energy of body at maximum height
View SolutionA body is projected from ground with velocity u making an angle θ with horizontal. Horizontal range of body is four time to maximum height attained by body. Find out
(i) angle of projection
(ii) Range and maximum height in terms of u
(iii) ratio of kinetic energy to potential energy of body at maximum height
View Solution
Knowledge Check
A particle is projected from the ground with velocity u at angle θ with horizontal.The horizontal range,maximum height and time of flight are R,H and T respectively.Now keeping u as fixed, θ is varied from 30∘ to 60∘.Then
AR will first increase.H will increase and T will decreaseBR will first increase.than decrease while H and T both will increaseCR will decrease while H and T will increaseDR will increase while H and T will decreaseA particle is projected from ground with speed u and at an angle θ with horizontal. If at maximum height from ground, the speed of particle is 1/2 times of its initial velocity of projection, then find its maximum height attained.
Au2gB2u2gCu22gD3u28gA particle is projected with a velocity u making an angle θ with the horizontal. At any instant its velocity becomes v which is perpendicular to the initial velocity u. Then v is
AucosθButanθCusecθDucotθ
A particle is projected from ground with speed u and at an angle θ with horizontal. If at maximum height from ground, the speed of particle is 1/2 times of its initial velocity of projection, then find its maximum height attained.
View SolutionA particle is projected with a velocity u making an angle θ with the horizontal. At any instant its velocity becomes v which is perpendicular to the initial velocity u. Then v is
View SolutionA particle is projected form ground with velocity u ar angle θ from horizontal. Match the following two columns.
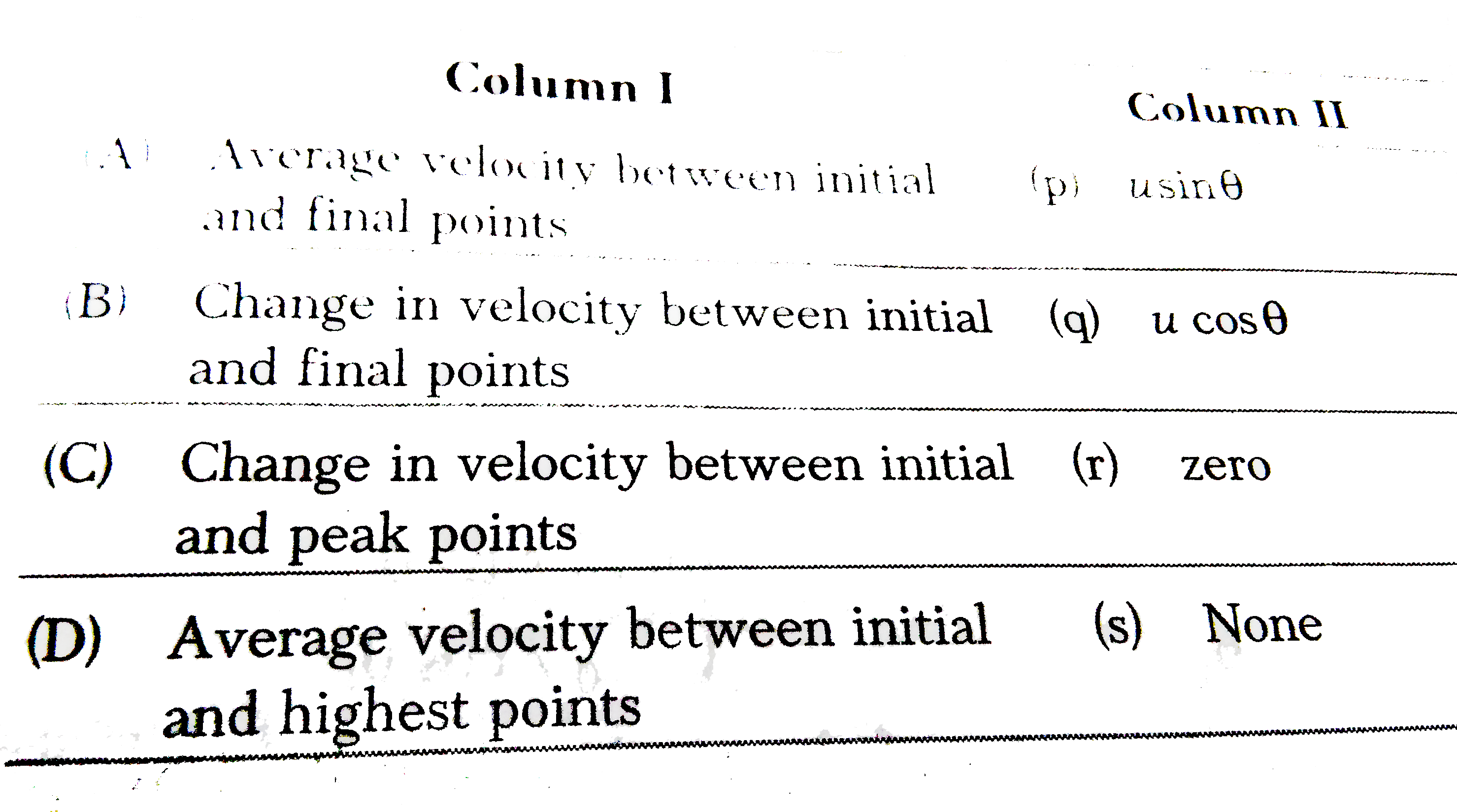
View SolutionA particle is projected form ground with velocity u ar angle θ from horizontal. Match the following two columns.
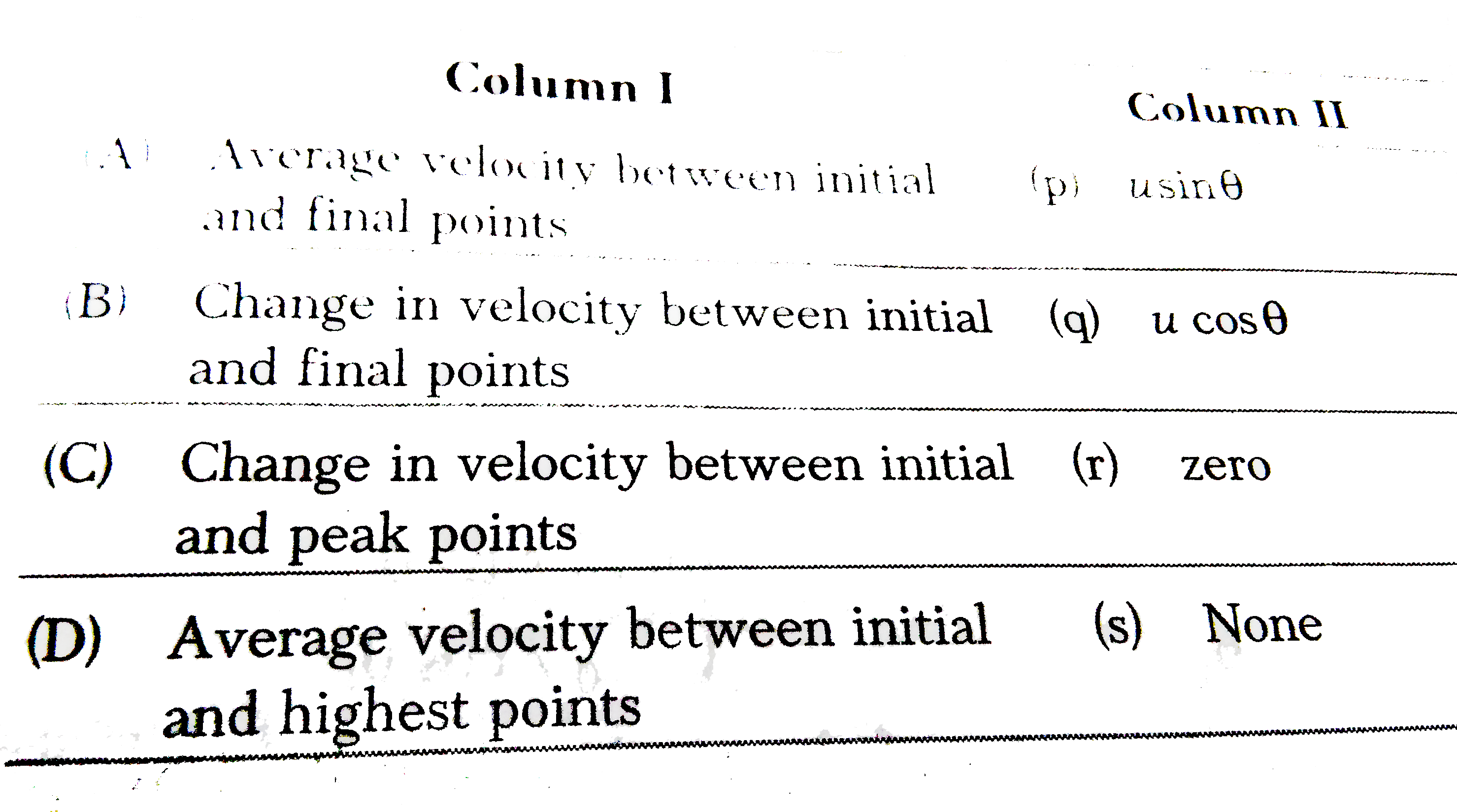
View SolutionA particle is projected with initial velocity u making an angle α with the horizontal, its time of flight will be given by
View Solution
