A particle is projected with a velocity u making an angle θ with the horizontal. At any instant its velocity becomes v which is perpendicular to the initial velocity u. Then v is
ucosθ
utanθ
ucotθ
usecθ
The correct Answer is:C
To solve the problem, we need to analyze the motion of a particle projected at an angle θ with an initial velocity u. The key point is that at some instant, the velocity v of the particle becomes perpendicular to the initial velocity u. We will derive the expression for v step by step.
1. Understanding the Initial Conditions:
- A particle is projected with an initial velocity u at an angle θ with the horizontal.
- The initial velocity can be resolved into two components:
- Horizontal component: ux=ucosθ
- Vertical component: uy=usinθ
2. Condition for Perpendicular Velocities:
- At a certain instant, the velocity v of the particle becomes perpendicular to the initial velocity u.
- If the angle between the initial velocity u and the velocity v is 90 degrees, then the angle between the horizontal and the new velocity v can be expressed as 90−θ.
3. Resolving the New Velocity:
- The new velocity v can also be resolved into components:
- Horizontal component: vx=vcos(90−θ)=vsinθ
- Vertical component: vy=vsin(90−θ)=vcosθ
4. Using the Horizontal Component:
- Since there is no acceleration in the horizontal direction (assuming no air resistance), the horizontal component of the velocity remains constant:
ux=vx
Therefore,
ucosθ=vsinθ
5. Solving for v:
- Rearranging the equation gives:
v=ucosθsinθ
- This can be simplified using the cotangent function:
v=ucotθ
Final Result:
Thus, the expression for v when it is perpendicular to the initial velocity u is:
v=ucotθ
- A particle is projected with an initial velocity u at an angle θ with the horizontal.
- The initial velocity can be resolved into two components:
- Horizontal component: ux=ucosθ
- Vertical component: uy=usinθ
- At a certain instant, the velocity v of the particle becomes perpendicular to the initial velocity u.
- If the angle between the initial velocity u and the velocity v is 90 degrees, then the angle between the horizontal and the new velocity v can be expressed as 90−θ.
- The new velocity v can also be resolved into components:
- Horizontal component: vx=vcos(90−θ)=vsinθ
- Vertical component: vy=vsin(90−θ)=vcosθ
- Since there is no acceleration in the horizontal direction (assuming no air resistance), the horizontal component of the velocity remains constant:
ux=vx
Therefore,
ucosθ=vsinθ
- Rearranging the equation gives:
v=ucosθsinθ
- This can be simplified using the cotangent function:
v=ucotθ
Thus, the expression for v when it is perpendicular to the initial velocity u is:
v=ucotθ
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-3
40 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-1
99 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
A particle is projected with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
View SolutionA particle is projected from the ground with velocity u making an angle θ with the horizontal. At half of its maximum heights,
View SolutionA particle is fired with velocity u making angle θ with the horizontal.What is the change in velocity when it is at the highest point?
View SolutionA particle is projected with velocity u at angle θ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View SolutionA particle is projected with velocity u at angle θ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
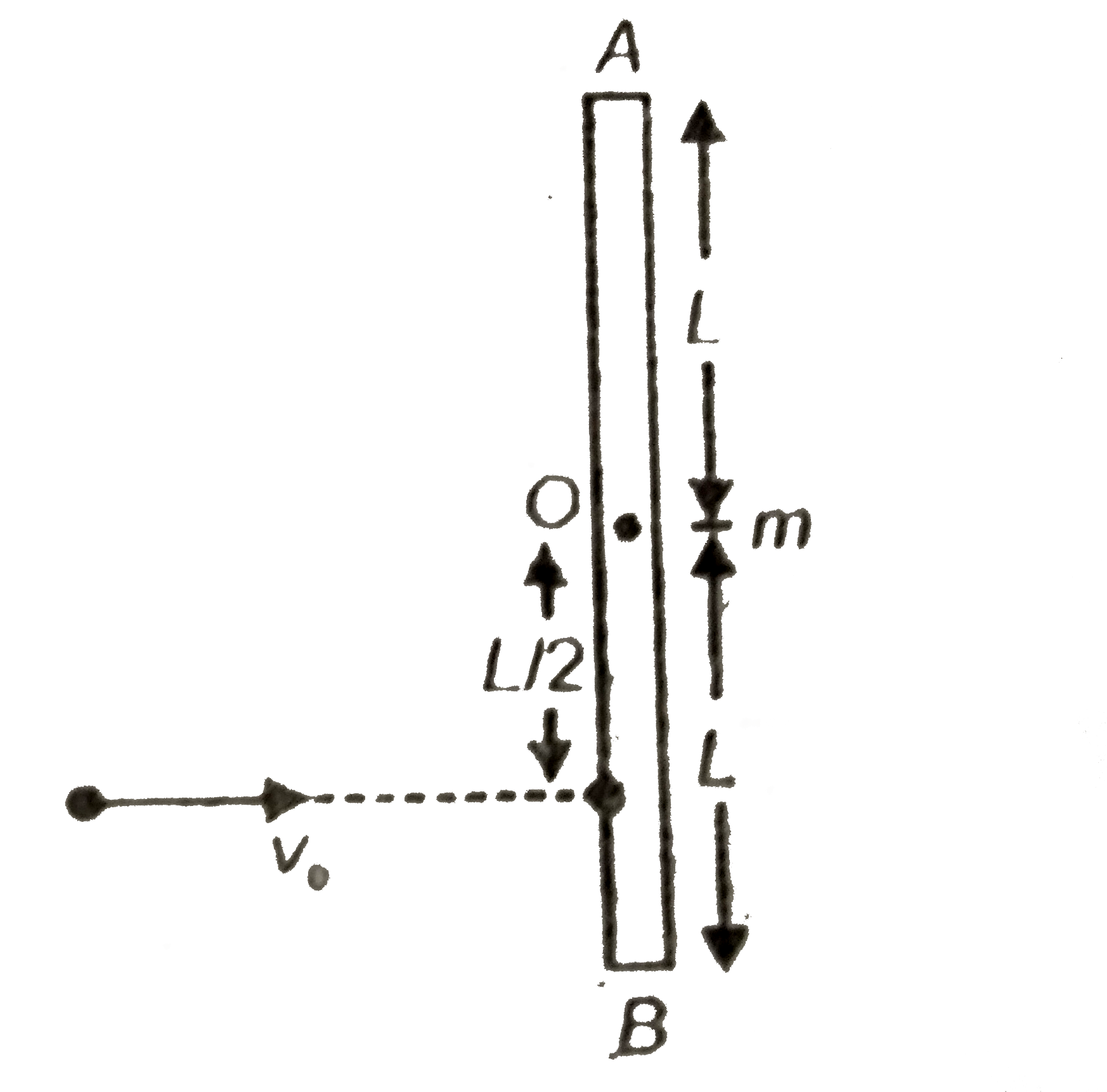
Distance of point P on rod from B which is at rest immediately afte collision is
View SolutionA particle is projected with velocity v at an angle θ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
View SolutionA particle is projected form ground with velocity u ar angle θ from horizontal. Match the following two columns.

View Solution
