Twenty identical cubical blocks each of mass 100 gm and of side 10 cm are lying on a horizontal surface. Work done in piling them one above the other is,
The correct Answer is:C
Similar Questions
If n number of identical cubes, each of mass m and side a lying on level ground. Find the work done in piling them one above the other.
View SolutionIdentical cubes each of mass 'm' and side T' are on the horizontal surface.Then the minimum amount of work done to arrange them one on the other is
View Solution
Knowledge Check
Question Stimulus
A cubical wooden block of side 10 cm and weight 100 N is resting on a horizontal surface. The pressure exerted on the surface by the block is
(##MPP_16_SH1_GKN_E03_052_Q01##)A10000 NB10000 Nm^(‐2)C1000 Nm‐2D100 Nm‐2The amount of work done in pumping water out of a cubical vessel of height 1 m is nearly (g=10ms−2)
A10 JB50 JC500 JD5000 JA bicycle chain of length 1.6m and of mass 1kg is lying on a horizontal floor. If g=10ms−2, the work done in lifting it with one end touching the floor and the other end 1.6m above the floor is
A10JB3.2JC8JD16J
A cubical block of mass 2 kg with each side of 2 cm is lying on the ground. What will be the pressure exerted by the block on the ground?
(Take g=9.8m/s2)
View SolutionA force of 100 N is applied horizontally on a block of mass 10 kg placed on a horizontal floor of coefficient of friction 0.5, The acceleration of the block is (takeg=10ms−2)
View SolutionA cubical block of wood of side 5 cm is placed on a table. Find the thrust by the block wood on the table, if density of wood is 5gcm−3 and g is 10 ms−2.
View SolutionA block of mass m = 10 kg is pulled by a force F = 100 N at an angle θ=30∘ with the horizontal along a smooth horizontal surface. What is the acceleration of the block? (g=10m/s2)
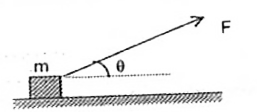
View SolutionA block of mass m = 10 kg is pulled by a force F = 100 N at an angle θ=30∘ with the horizontal along a smooth horizontal surface. What is the acceleration of the block? (g=10m/s2)

View Solution
