Three particles each of mass 'm' are located at the three vertices of an equilaterial triangle of side 'a'. If the system is revolving in a uniform circle due to their mutual force of attraction, then the angular velocity of each particle is
√Gm3a3
√3Gma3
√Gm23a3
√Gm2a3
The correct Answer is:B
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - GRAVITATION (ACCELERATION DUE TO GRAVITY)10videos
APPENDICES
- BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - GRAVITATION (ACCELERATION DUE TO GRAVITY BELOW AND ABOVE SURFACE OF THE EARTH)18videos
APPENDICES
- BOOK - AAKASH SERIESCHAPTER - APPENDICES EXERCISE - GRAVITATION (KEPLER.S LAWS)9videos
APPENDICES
- BOOK - AAKASH SERIESCHAPTER - CALORIMETRY EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) (LECTURE SHEET (ADVANCED)(Matrix Type Questions)1videos
CALORIMETRY
Similar Questions
Four particles each of mass 'm' are located at the four corners of a sqaure of side a. If the system is revolving in a circle due to thei mutual force of attraction then the angular velocity and time period of each particle is
View SolutionThree identical particles, each of mass m, are located in space at the vertices of an equilateral triangle of side length a. They are revolving in a circular orbital under mutual ravitational attraction. Find the speed of each particle. Find the acceleration of the centre of mass of a system comprising of any two particles. Assume that one of the particles suddenly loses its ability to exert gravitational force. Find the velocity of the centre of mass of the system of other two particles after this.
View Solution
Knowledge Check
- Question 1 - Select One
Three particles each of mass m are palced at the corners of an equilateral triangle of side b. The gravitational potential energy of the system of particle is
A3GMa2B3GM2aC−3GM2a2D3GM2a - Question 2 - Select One
Three particle each of mass m, are located at the vertices of an equilateral triangle of side a. At what speed must they move if they all revolve under the influence of their gravitational force of attraction in a circular orbit circumscribing the triangle while still preserving the equilateral triangle ?
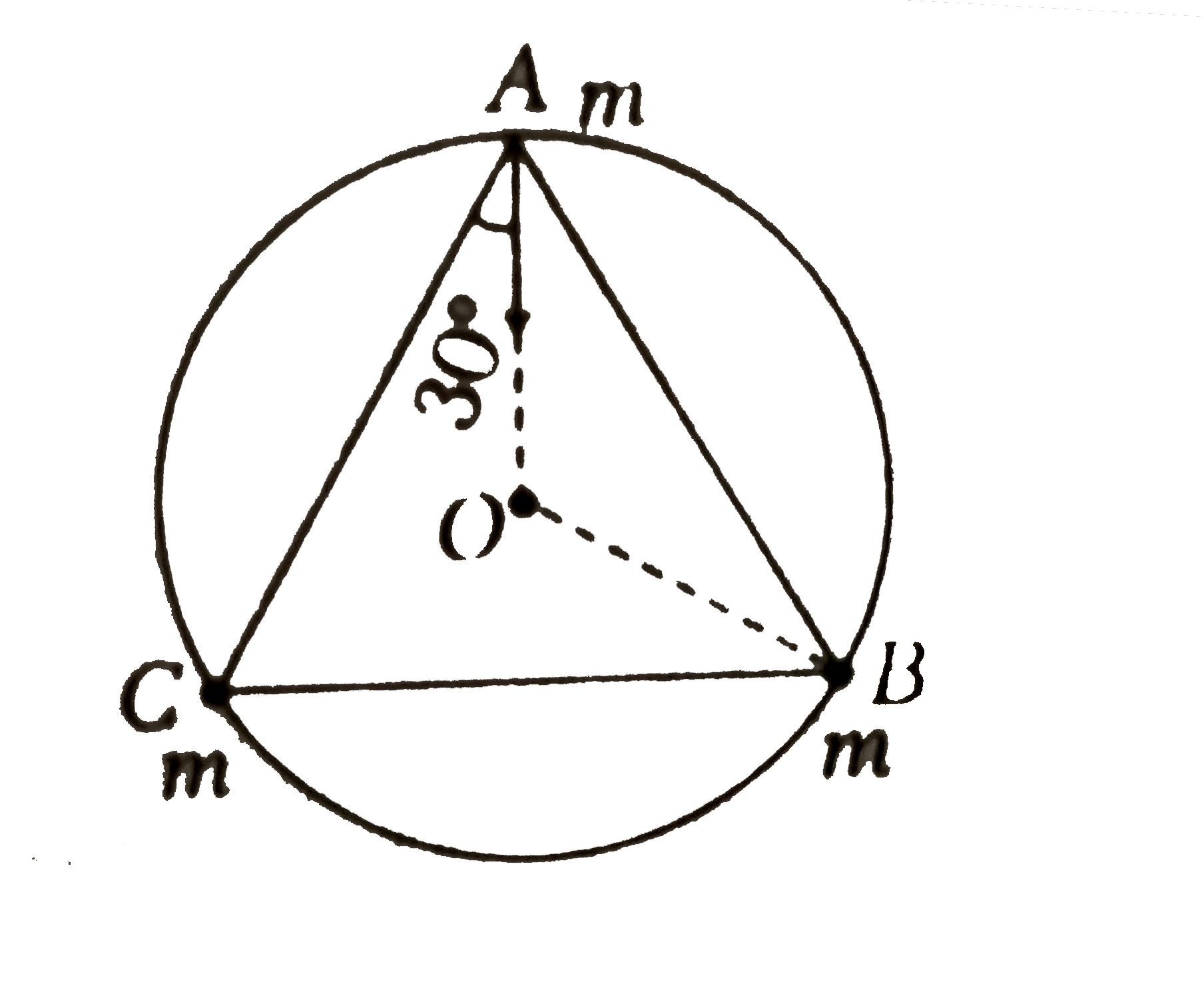 A√GmaB√2GmaC√3GmaD√4Gma
A√GmaB√2GmaC√3GmaD√4Gma - Question 3 - Select One
Three particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
AzeroB3GML2C9GML2D2GML2
Three particle each of mass m, are located at the vertices of an equilateral triangle of side a. At what speed must they move if they all revolve under the influence of their gravitational force of attraction in a circular orbit circumscribing the triangle while still preserving the equilateral triangle ?
 View Solution
View SolutionThree particles, each of mass m, are situated at the situated at the vertices of an equilateral triangle of side 'a'. The only forces acting on the particles are their mutual gravitational forces. It is intended that each particle moves along a circle while maintaining their original separation 'a'. Determine the initial velocity that should be given to each particle and the time period of the circular motion. The resultant force on particle at A due to other two particles is
View SolutionThree particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
View SolutionThree particles each of mass m are palced at the corners of an equilateral triangle of side b. The gravitational potential energy of the system of particle is
View SolutionThree particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
View Solution

