Two masses kg and kg passes over a pulley. Find the ratio of the masses so that string passes over the pulley will just start slipping over is surface. The friction coefficient between the string and pulley surface is 0.2
From the ideas of laws of motion, for the two masses,
and
and if string starts slipping we have
solving the above equations
if string just slipps we can use a=0, thus we have
Similar Questions
Two masses m1 kg and m2 kg passes over an atwoods machine. Find the ratio of masses m1 and m2 so that string passing over the pulley will just start slipping over its surface. The friction coefficient between the string and pulley surface is 0.2.
View SolutionA situation is shown in figure-2.15, Find the acceleration of masses m1 abd m2 mass of pulley is mP. Consider the string going over the pulley is massless and frictionless.

View Solution
Knowledge Check
Suppose we consider friction between string and the pulley while still considering the string to be massless. So, in such a theoretical case, the tension in the string in contant with the pulley will not be constant and its variation is calculated as follows.
If the string is just on the verge of slipping on the pulley, then friction acting is limiting and if T2>T1 then friction will act towards T1 in tangential direction as shown.

dN=(T+df)sin(dθ/2)+(T+dT)sin(dθ/2)
dN=Tsin(dθ/2)+dfsin(d∂/2)+Tsin(dθ/2)+dTsin(dθ/2)
dN≈2Tsin(dθ/2)
dN≈2Tdθ2
dN=Tdθ ........(1)
Alsso, (T+df)cos(dθ2)=(T+dT)cos(dθ2)
Tcos(dθ2)+dfcos(dθ2)=Tcos(dθ2)1dTcos(dθ2)
df=dT=μdN.........(2)
from (1) & (2)
dT=μTdθ
∫T2T1dTT=μ∫θ0dθ
ln(T2T1)=μθ
T2=T1eμθ, where θ is the angle of contact between the string and the pulley Based on above information, answer the following questions.
Two masses m1kg and m2kg passes over an atwood machine. Find the ratio of masses m1 and m2 so that string passing over the pulley will just start slipping over its surface. The friction coefficient between the string and pulley surface is 0.2.Ae0.2πBe0.2C0.2De0.4πTwo blocks of masses M1=4 kg and M2=6kg are connected by a string of negligible mass passing over a frictionless pulley as shown in the figure below. The coefficient of friction between the block M1 and the horizontal surface is 0.4. when the system is released, the masses M1 and M2 start accelrating. What additional mass m should be placed over M1 so that the masses (M1+m) slide with a uniform speed?
 A12 kgB11 kgC10 kgDkg
A12 kgB11 kgC10 kgDkgTwo masses M and m(M>m) are joined by a light string passing over a smooth light pulley.
 AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g
AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g
two masses 2m and m are attached to the the ends of a string while passing over a smooth Pulley of mass m and radius R. The ratio of tensions in both the strings is
_PHY_E05_245_Q01.png)
View SolutionTwo masses M1 and M2 are attached to the ends of a light string which passes over a massless pulley attached to the top of a double inclined smooth plane of angles of inclination α and β.The tension in the string is :
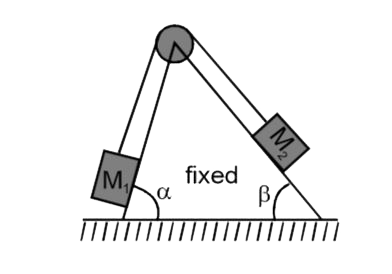
View SolutionIn figure m1=1kg and m2=4kg Find the mass m of the hanging block which will provent the smaller block from slipping over the triangular block .All the surface are frictionless and the string and the pulleys are light

View SolutionTwo masses m1=4kgandm2=2kg are connected with an nextansible , massless string that passes over a frictionless pulley and through a slit as, shown the string is vertical upon by a conatant friction force 10 N by the slit as it moves (use g=10m/s2
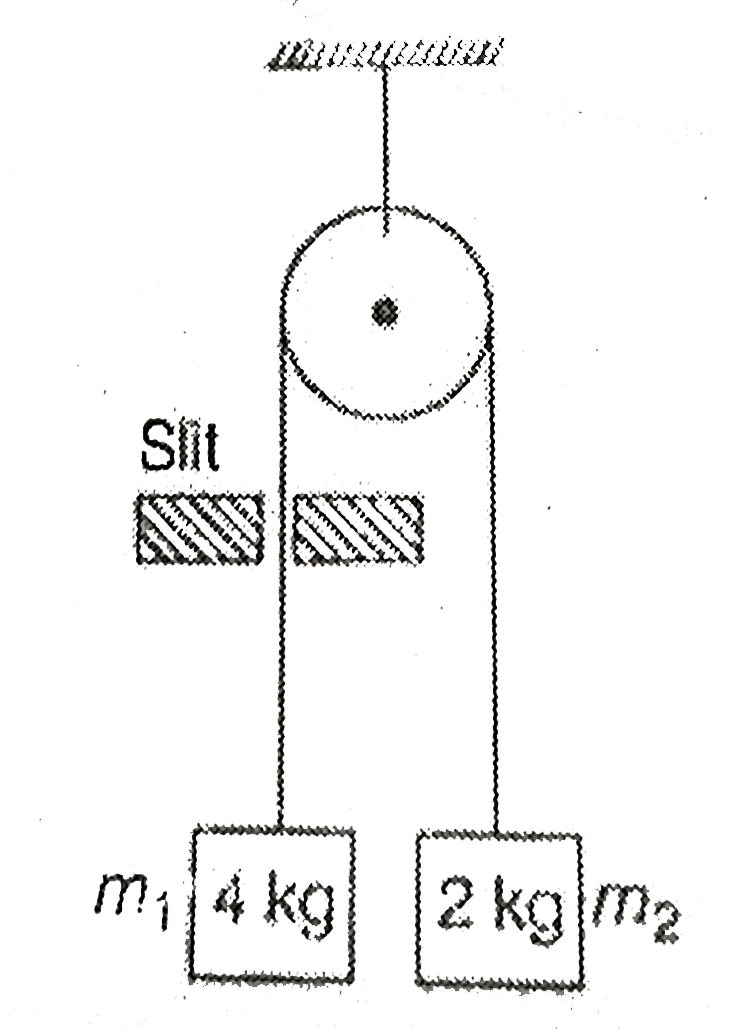
View SolutionTwo masses m1 and m2 are connected to the ends of a massless string that passes over a pulley fixed at the top of a double incline as shown. Assuming m1>m2 acceleration of the system is:

View Solution
