A uniform solid sphere of mass m and radius R spinning with an angular speed oh, is kept at the junction of the horizontal and vertical surfaces. If the coefficienty of friction between all contacting surface is . find the 1) time after which the sphere will stop rotating. (ii) number of rotations of the sphere before it stops rotating,

(i)2ω0(1+2μR)5g(1+μ), (ii)ω2o(1+μ2)+R10πg(1+μ)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for Descriptive Answers
20 Videos
- ROTATIONAL MECHANICSBOOK - AAKASH SERIESCHAPTER - ROTATIONAL MECHANICSEXERCISE - Numerical Exercise (LEVEL-1)
18 Videos
- ROTATIONAL DYNAMICS BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Integer Type Questions
7 Videos
- SIMPLE HARMONIC MOTION BOOK - AAKASH SERIESCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II)(PRACTICE SHEET (ADVANCED)) (INTEGER TYPE QUESTIONS)
3 Videos
Similar Questions
A ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
View SolutionA uniform disc of mass m and radius R I rotated about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. It is placed on a rough horizontal plane with the axis of the disc keeping vertical. Coefficnet of friction between te disc and the surface is μ, find
(a). The time when disc stops rotating
(b). The angle rotated by the disc before stopping.
View Solution
Knowledge Check
A ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
Aω0μR2gBω0g2μRC2ω0RμgDω0R2μgA solid sphere of mass M and radius R spins about an axis passing through its centre making 600 rpm. Its kinetic energy of rotation is
A25π2MRB25πM2R2C80πMRD80π2MR2
A uniform disc of mass m and radius R is rotated about an axis passing through its center and perpendicular to its plane with an angular velocity ω. It is placed on a rough horizontal plane with the axis of the disc keeping vertical. Coefficient of friction between the disc and the surface is μ, find
(a). The time when disc stops rotating
(b). The angle rotated by the disc before stopping.
View SolutionA solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is

View SolutionA solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is

View SolutionA solid sphere of radius 2.45m is rotating with an angular speed of 10rad/s. When this rotating sphere is placed on a rough horizontal surface then after sometime it starts pure rolling. Find the linear speed of the sphere after it starts pure rolling.
View SolutionA solid sphere of radius 2.45m is rotating with an angular speed of 10rad/s. When this rotating sphere is placed on a rough horizontal surface then after sometime it starts pure rolling. Find the linear speed of the sphere after it starts pure rolling.
View SolutionA solid ball of mass m and radius r spinning with angular velocity ω falls on a horizontal slab of mass M with rough upper surface (coefficient of friction μ) and smooth lower surface. Immediately after collision the normal component of velocity of the ball remains half of its value just before collision and it stops spinning. Find the velocity (in m/s) of the sphere in horizontal direction immediately after the impact (given: Rω=5).
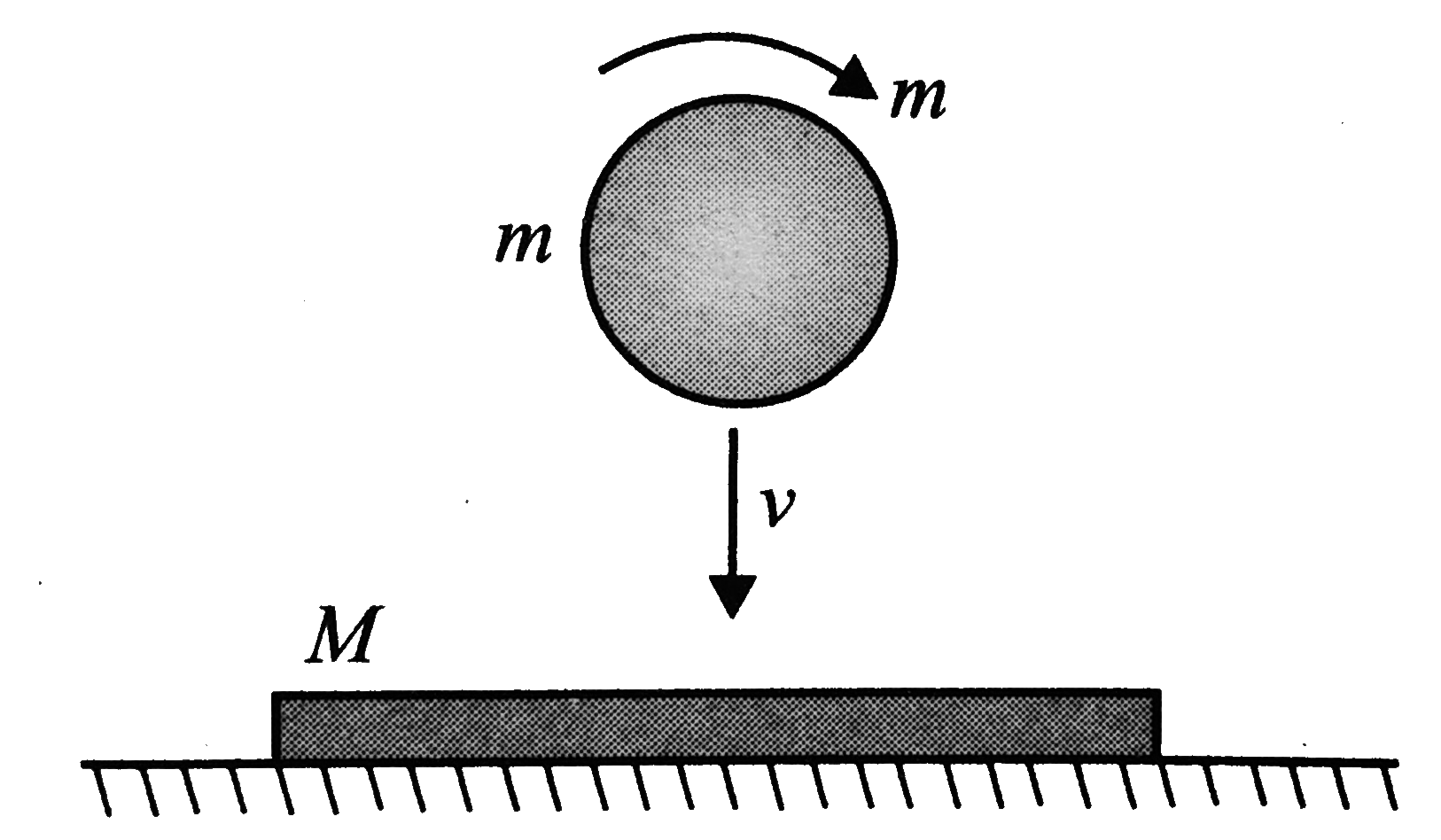
View Solution
