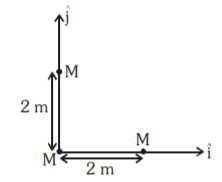
Three identical spheres , each of mass M , are placed at the corners of a right angled triangle with mutually perpendicular sides equal to 2 m . Taking their point of intersection as the origin , find the position vector of centre of mass

x-coordination =
Again
or m
y-coordinate =
Position vector of centre of mass =
Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS )
140 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - CHECK YOUR NEET VITALS
14 Videos
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)
24 Videos
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - AIPMT / NEET MCQs
43 Videos
Similar Questions
Three identical spheres each of mass M are placed at corners of right angle triangle with mutually perpendicular sides equal to 2m. Taking point of intersection of two mutually perpendicular sides as origin find position vector center of mass
View SolutionThree identical spheres of mass M each are placed at the corners of an equilateral triangle of side 2 m. Taking one of the corners as the origin, the position vector of the centre of mass is
View Solution
Knowledge Check
Three identical spheres each of mass M are placed at corners of right angle triangle with mutually perpendicular sides equal to 2m. Taking point of intersection of two mutually perpendicular sides as origin find position vector center of mass
 A2(ˆi+ˆj)B(ˆi+ˆj)C2ˆi+ˆj3D4ˆi+ˆj3
A2(ˆi+ˆj)B(ˆi+ˆj)C2ˆi+ˆj3D4ˆi+ˆj3Three identical spheres each of mass M are placed at corners of right angle triangle with mutually perpendicular sides equal to 2m. Taking point of intersection of two mutually perpendicular sides as origin find position vector center of mass
 A(##PW_NEET_45_DAY_PHY_C06_E03_004_Q01##)B23(ˆi+ˆj)C43(ˆi+ˆj)D2(ˆi+ˆj)
A(##PW_NEET_45_DAY_PHY_C06_E03_004_Q01##)B23(ˆi+ˆj)C43(ˆi+ˆj)D2(ˆi+ˆj)Three equal masses each of 50 g, are placed at the corners of a right angled isoceles triangle whose two equal sides are 5 cm each. The position of the centre of mass of the system is
Ax=5 cm,y=5 cmBx=53 cm,y=5 cmCx=53 cm,y=52 cmDx=53 cm,y=53 cm
Three particle each of 1 kg mass are placed at corners of a right angled triangle AOB, 'O' being the origin of coordinate system (OA and OB along the x-direction and +ve y-direction). If OA = OB = 1m, the position vector of centre of mass (in metres) is
View SolutionThree identical spheres of mass M each are placed at the corners of an equilateral triangle of side 2 m. Taking one of the corners as the origin, the position vector of the centre of mass is
View SolutionThree identical spheres of mass m each are placed at the corners of an equilateral triangle of side 2m taking one of the corner as the origin the position vector of the centre of mass is
View SolutionThree identical spheres of mass m each are placed at the corners of an equilateral triangle of side 2m taking one of the corner as the origin the position vector of the centre of mass is
View SolutionFour identical spheres each of mass m are placed at the corner of square of side 2 m. Taking the point of intersection of the diagonals as the orgin the coordinates of the centre of mass are ?
View Solution
