Three bricks each of length L and mass M are arranged as shown from the wall. The distance of the centre of mass of the system from the wall is

The correct Answer is:D

From figure ,
Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - CHECK YOUR NEET VITALS
14 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)
24 Videos
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - AIPMT / NEET MCQs
43 Videos
Similar Questions
Two uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View Solution
Knowledge Check
Two point masses m and M are separated by a distance L . The distance of the centre of mass of the system from m is
AL(m/M)BL(M/m)CL(Mm+M)DL(mm+M)Two point masses m and M are separated bya distance L . The distance of the centre of mass of the system from m is
AL(m/M)BL(M/m)CL(Mm+M)DL(mm+M)Three rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY¢ will be
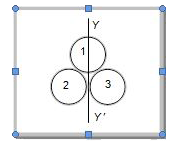 A3MR2B32MR2C5MR2D72MR2
A3MR2B32MR2C5MR2D72MR2
Three identical rods each of length L and mass m are joined to form a U -shape as shown in figure. The distance of centre of mass of combined system from the corner .O. is
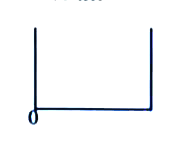
View SolutionSix rods of the same mass m and length ? are arranged as shown in figure. Calculate the coordinate of the centre of mass of the system:- У >X
View SolutionThree spheres, each mass M and radius R, are arranged as shown in the figure . The moment of inertia of the system will be

View SolutionThree identical particles each of mass 0.1kg are arranged at three corners of a square of side √2m. The distance of the centre of mass from the fourth corners is
View SolutionThree identicle particle each of mass 1kg are placed with their centres on a straight line. Their centres are marked A,BandC respectively. The distance of centre of mass of the system from A is.
View Solution
