A cricket bat is cut at the location of its centre of mass as shown. Then

the two pieces will have the same mass
the bottom piece will have larger mass
the handle piece will have larger mass
mass of handle piece is double the mass of bottom piece
The correct Answer is:B
Centre of mass is closer to massive part of the body therefore the bottom piece of bat have larger mass .
Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - CHECK YOUR NEET VITALS
14 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)
24 Videos
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - AIPMT / NEET MCQs
43 Videos
Similar Questions
Knowledge Check
A baseball bat of uniform density is cut at the location of its center of mass as shown in figure. The piece with the smaller mass is
 Athe piece on the rightBthe piece on the leftCBoth pieces have the same massDimpossible to determine.
Athe piece on the rightBthe piece on the leftCBoth pieces have the same massDimpossible to determine.From a solid cylined of length 4R and radius R, two hemispheres of radius R and R2 are cut from both the ends as shown. The location of new centre of mass from point O is approximately
 A3RB2RC3R2DR
A3RB2RC3R2DR
A cricket bat is cut through its centre of mass into two parts as shown. Then, state whether both parts are of same mass or not, Also explain reason.
View SolutionWhat is the location of the centre of mass of a uniform triangular lamina ?
View SolutionLocate the position of the centre of mass of a hemisphere of radius R as shown in the following figure:

View SolutionA square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be
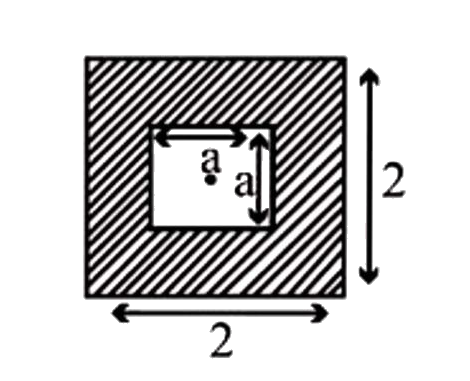
View SolutionA square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be

View SolutionFour particles of masses m, m, 2m and 2m are placed at the corners of a square of side a, as shown in fig. Locate the centre of mass.
View Solution


