For the given uniform square lamina ABCD, whose centre is O,

A

$I_{A C} = \sqrt{2} I_{E F}$

B

$\sqrt{2} I_{A C} = I_{E F}$

C

$I_{A D} = 3 I_{E F}$

D

$I_{A C} = I_{E F}$

Text Solution

Verified by Experts

The correct Answer is:D

Let I be the moment of inertia of the square lamina about an axis through O and perpendicular to its plane . Then by perpendicular axes theorem ,
$I_{A C} + I_{B D} = I$
or $I_{A C} = \frac{I}{2} [∵ I_{A C} = I_{B D}]$
Again by perpendicular axes theorem ,
$I_{E F} + I_{G H} = I$
or $I_{E F} = \frac{I}{2} [∵ I_{E F} = I_{G H}]$
Hence $I_{A} C = I_{E} F$

Updated on:21/07/2023

|

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

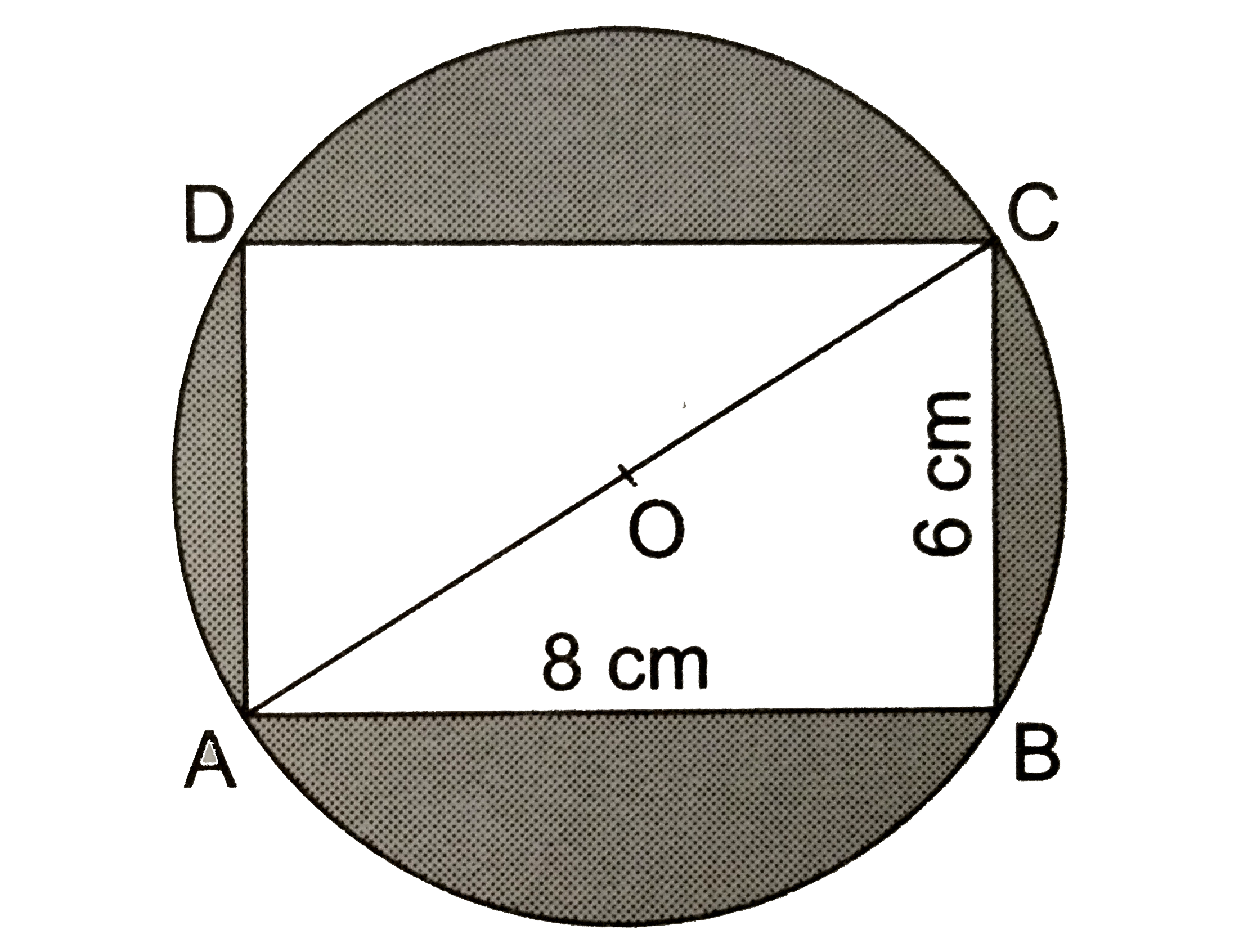
In the adjoining diagram ABCD is a square with side 'a' cm. In the diagram the area of the larger circle with centre 'O' is equal to the sum of the areas of all the rest four circles with equal radii, whose centres are P,Q,R and S . What is the ratio between the side of square and radius of a smaller circle ?

A $(2 \sqrt{2} + 3)$
B $(2 + 3 \sqrt{2})$
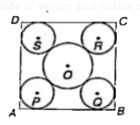
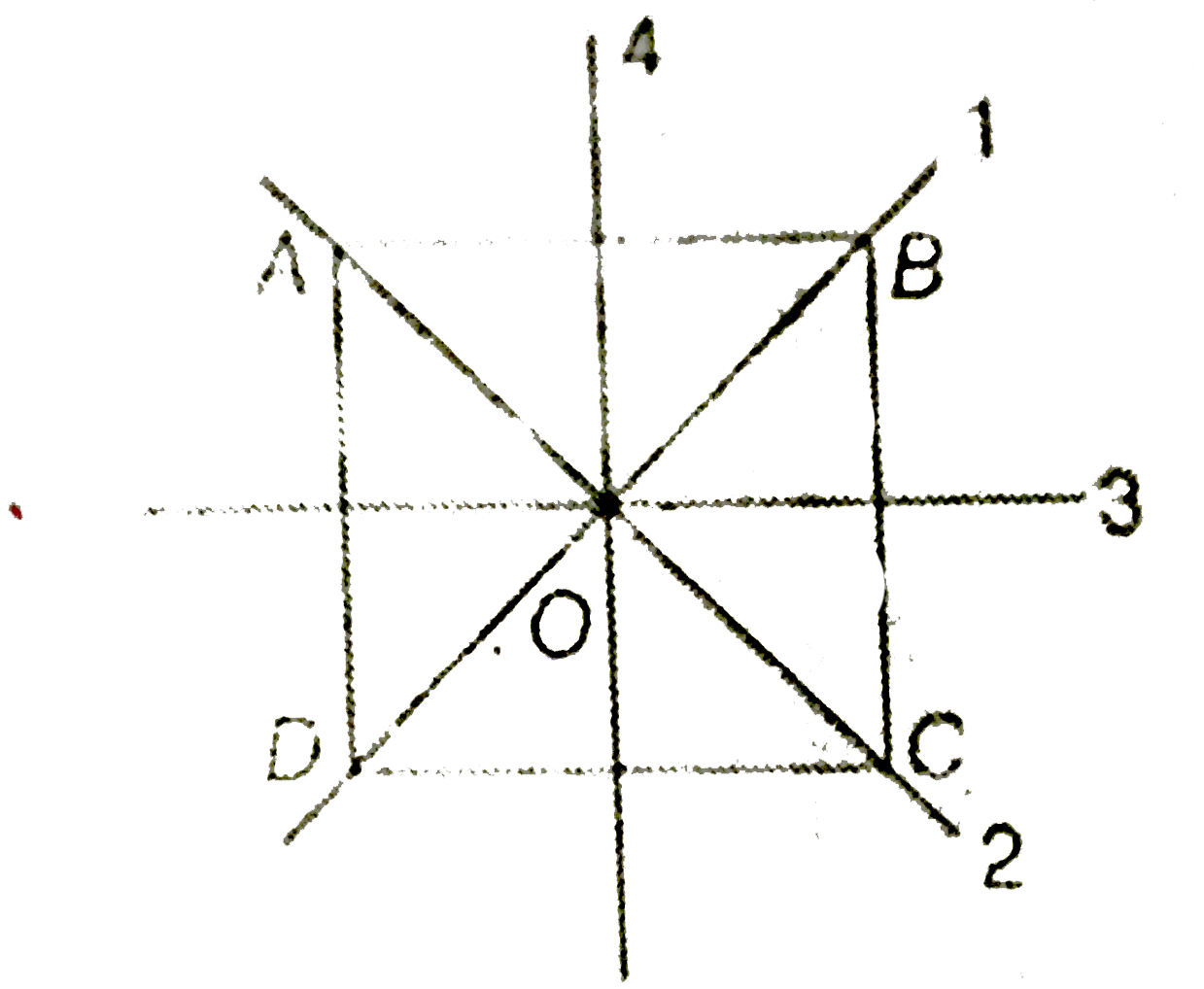
C $(4 + 3 \sqrt{2})$
Dcan't be determined
The moment of inertia of a thin square plate ABCD, as shown A in the figure, of uniform thickness about an axis passing through the centre O and perpendicular to the plane of

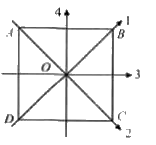A $l_{1} + l_{2}$
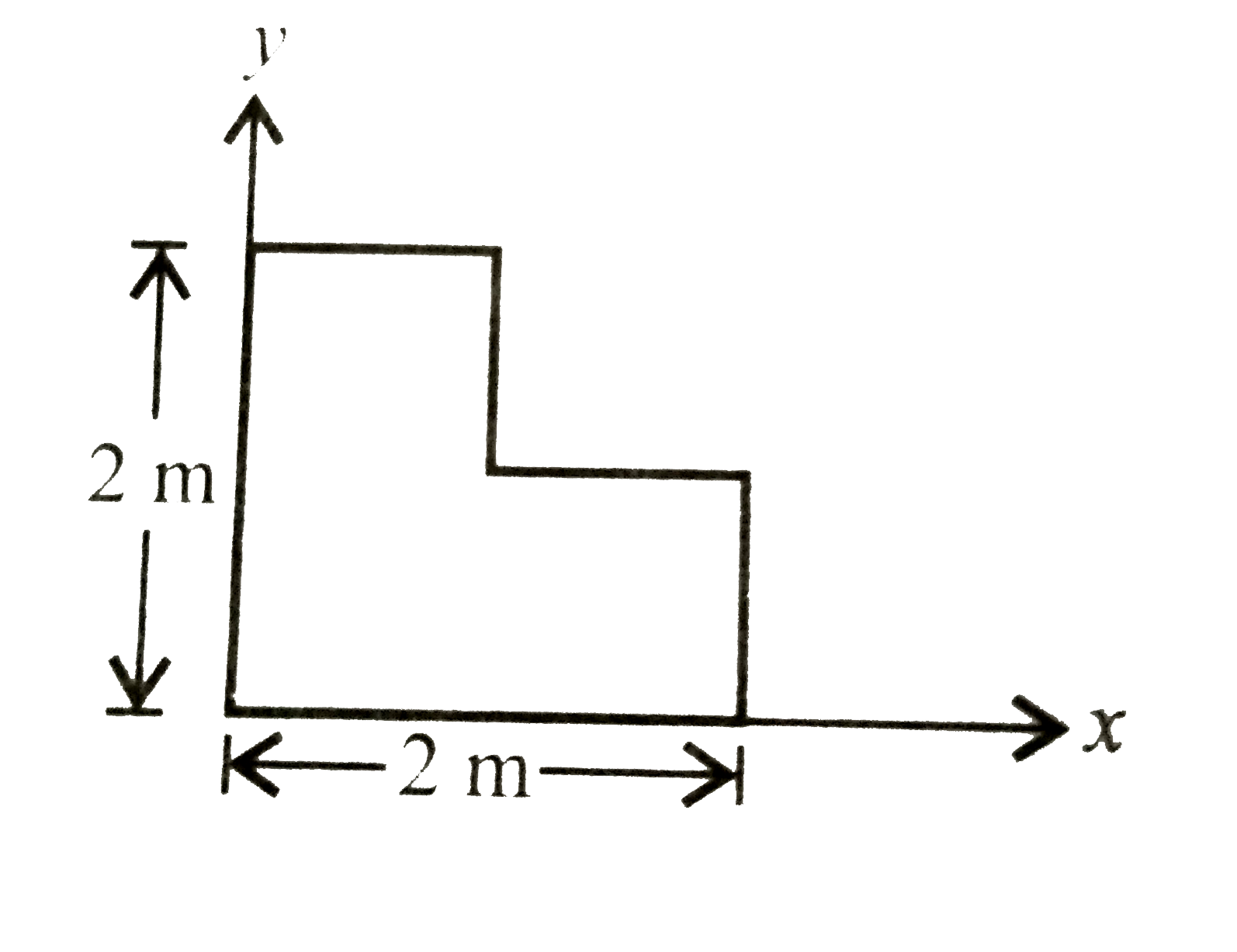
B $l_{3} + l_{4}$
C $l_{1} + l_{3}$
D $l_{1} + l_{2} + l_{3} + l_{4}$ ltbRgt where $l_{1}, l_{2}, l_{3}$ and $l_{4}$ are respectively the moments of inertia about axis 1, 2, 3 and 4 which are in the plane of the plate.
The x, y coordinates of the centre of mass of a uniform L-shaped lamina of mass 3 kg is

A(5/6 m, 5/6 m)
B(1 m, 1 m)
C(6/5 m, 6/5 m)
D(2 m, 2m)

MTG GUIDE-MOTION OF SYSTEM OF PARTICLES AND RIGID BODY -NEET CAFE (TOPICWISE PRACTICE QUESTIONS )

Home
Ask Doubt
Profile