A block of mass m starting from rest slides down a smooth inclined plane of gradient e, fixed in a lift moving upwards with an acceleration an as shown in figure. If the base of the inclined plane has length L, the time taken by the block to slide from top to bottom of the inclined plane, will be

The correct Answer is:B
Acceleration along the inclined plane,
Slope length
using we get
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - NEET CAFÉ (TOPICWISE PRACTIVE QUESTIONS) (LAW OF CONSERVATION OF LINEAR MOMENTUM AND ITS APPLICATIONS)
6 Videos
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - NEET CAFÉ (TOPICWISE PRACTIVE QUESTIONS) (EQUILIBRIUM OF CONCURRENT FORCES)
7 Videos
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)
24 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - AIPMT/ NEET MCQs
31 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
Similar Questions
A particle slides down a smooth inclined plane of elevation θ fixed in an elevator going up with an acceleration a0. The base of the incline has a length L. Find the time taken by the particle to reach the bottom.
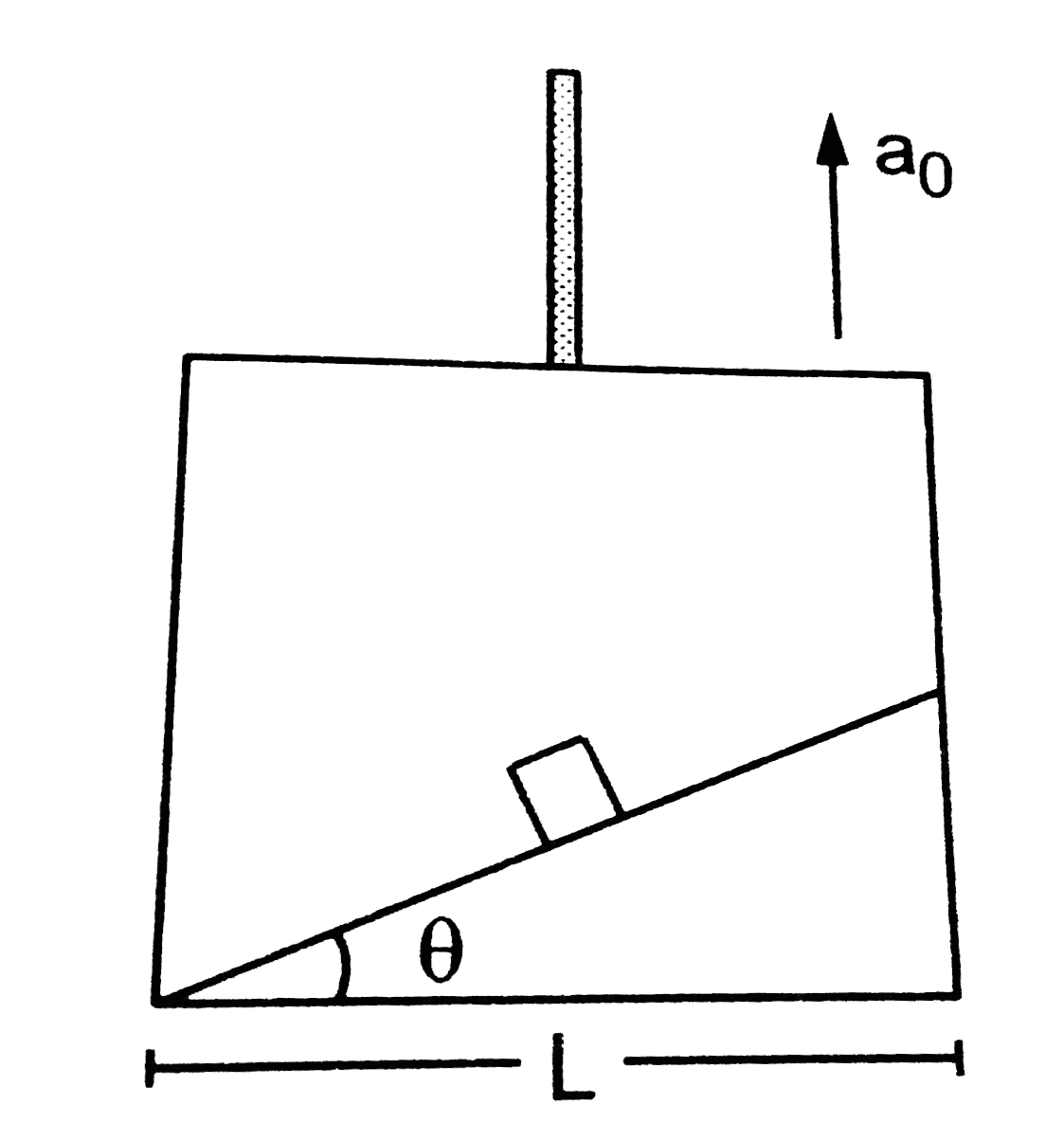
View SolutionA particle slides down a smooth inclined plane of elevation θ fixed in an elevator going up with an accelerationa0. The base of the incline has a length L.Find the time taken by the particle to reach the bottom.

View Solution
Knowledge Check
A particle slides down a smooth inclined plane of elevation , fixed in an elevator going up with an acceleration a0 (figure). The base of the incline has a length L. Find the time taken by the particle to reach to the bottom -
 A[2Lgsinθcosθ]1/2B[2L(g−a0)sinθcosθ]1/2C[2L(g+a0)cosθ]1/2D[2L(g+a0)sinθcosθ]1/2
A[2Lgsinθcosθ]1/2B[2L(g−a0)sinθcosθ]1/2C[2L(g+a0)cosθ]1/2D[2L(g+a0)sinθcosθ]1/2A particle slides down a smooth inclined plane of elevation fixed in an elevator going with an acceleration a as shown in the figure. The base of the incline has a length L.
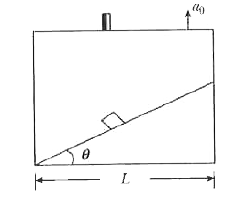
If the elevator going up with constant velocity, the time taken by the particle to reach the bottom isA(2L(gsinθcosθ))1/2B(2Lgsinθ)1/2C(2Lgcosθ)1/2DNone of these
A particle slides down a smooth in clined plane of elevation θ fixed in an elevastor going up with an accelerationa0. The base of the incline has a length L.Find the time taken by the particle to reach the bottom.

View SolutionA block slides down from top of a smooth inclined plane of elevation ● fixed in an elevator going up with an acceleration a0 The base of incline hs length L Find the time taken by the block to reach the bottom
 .
.
View SolutionA block slides down from top of a smooth inclined plane of elevation ● fixed in an elevator going up with an acceleration a0 The base of incline hs length L Find the time taken by the block to reach the bottom
 .
.
View SolutionA frictionless inclined plane of length l having inclination θ is placed inside a lift which is accelerating downward with on acceleration a (<g). If a block is allowed to move down the inclined plane, from rest, then the time taken by the block to slide from top of the inclined plane to the bottom of the inclined plane is
View SolutionA block is placed on an inclined plane moving towards right with an acceleration a0=g The length of the inclined plane is l0. All the surfaces are smooth Find the time taken by the block to reach from bottom to top.
 .
.
View SolutionIf the body starts from rest from the top of the rough inclined plane of length 1, time taken to reach the bottom of the plane is
View Solution
