A block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pully at the edge of the table and from its other end another block B of mass m2 is suspended. The coefficient of kinetic friction between the block and the table is H. When the block A is sliding on the table, the tension in the string is
m1m2(1+μk)g(m1+m2)
m1m2(1−μk)g(m1)+m2
(m2+μkm1)g(m1+m2)
(m2−μkm1)g(m1+m2)
The correct Answer is:A
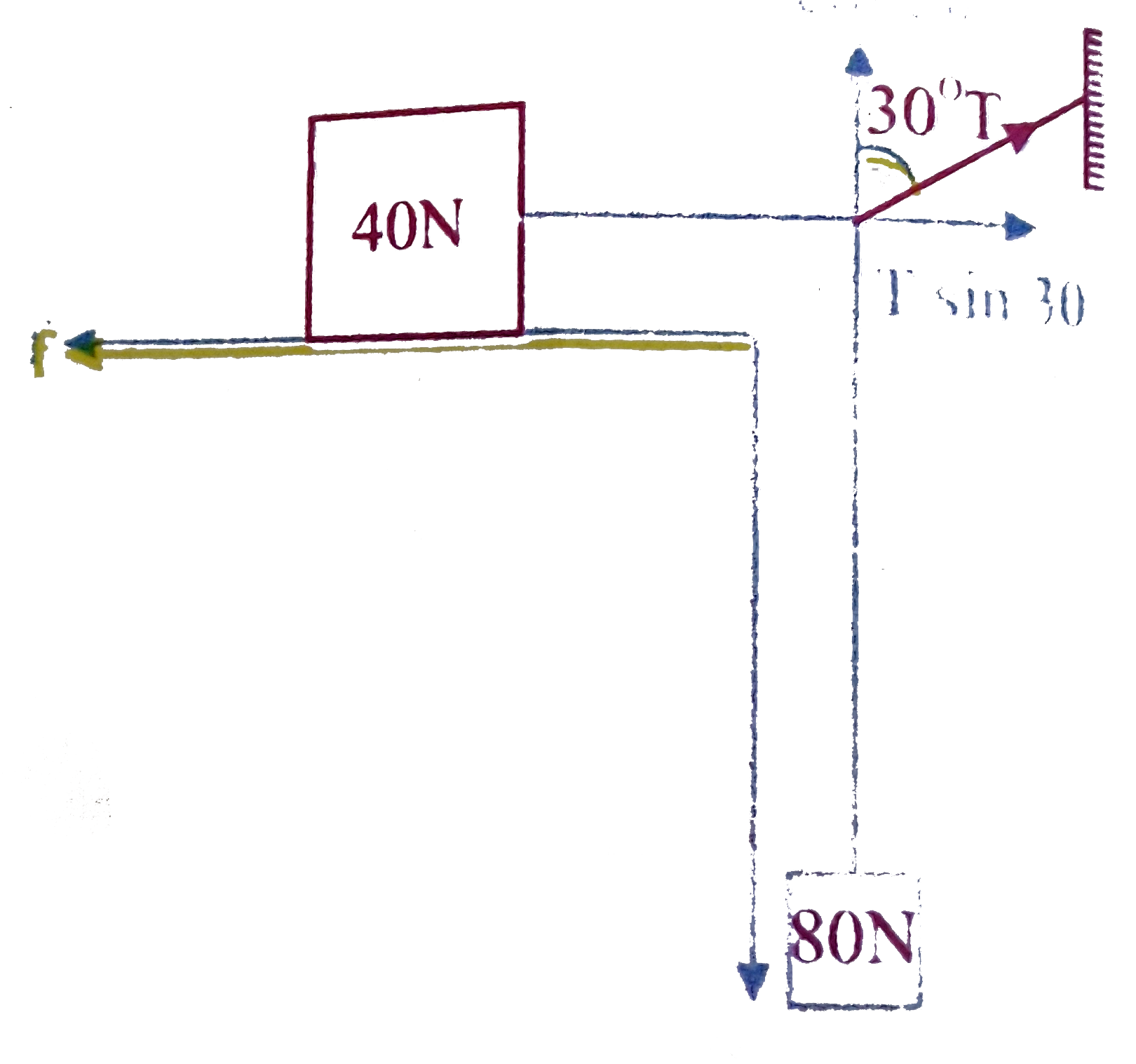
Given situation is shown in the figure
here ,N=m1g,f=μkN=μkm1g…(i)
Let a be the acceleation on blocks .
equation of motion for A and B
T−f=m1a…(ii)
m2g−T=m2a…(iii)
Adding equation (ii) and (iii)
we get
m2g−f=(m1+m2)a
a=m2g−fm1+m2
substiting value of a in equation (iii)
T=m2g−m2(m2g−f)m1+m2
=m1m2g+m1m2μsgm1+m2=m1m2(1+μs)gm1+m2 ( using (i))

Topper's Solved these Questions
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - CHECK YOUR NEET VITALS
22 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - AIPMT/ NEET MCQs
31 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
Similar Questions
A block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of table and from its other end another block B of mass m2 is suspended. The coefficient of knetic friction between the block and table is μk . When the block A is sliding on the table, the tension in the string is.
View SolutionA block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
View Solution
Knowledge Check
A block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of table and from its other end another block B of mass m2 is suspended. The coefficient of knetic friction between the block and table is μk . When the block A is sliding on the table, the tension in the string is.
A(m2+μkm1)gm1+m2B(m2−μkm1)gm1+m2Cm1m2(1+μk)g(m1+m2)Dm1m2(1−μk)g(m1+m2)A block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
Am2gm1+m2Bm1gm1+m2CgDm2gm1A block of mass 4 kg is resting on a horizontal table and a force of 10 N is applied on it in the horizontal direction. The coefficient of kinetic friction between the block and the table is 0.1. The work done in √20 s
ABy the applied force is 150 JBBy the frictional force is 60 JCBy the applied force and the net force are 150 J and 90 J respectivelyDAll are correct
A body of mass 20 kg is resting on a table. A light string is attached to it and passed over a smooth pulley at the edge of the table and a mass 3kg is attached at the free end. What is the acceleration of the system of the coefficient of kinetic friction between the mass and the table is 0.04 ? What is the tension in the string ?
View SolutionA block on table shown in is just on the edge of slipping Find the coefficient of static friction between the blocks and table
 .
.
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
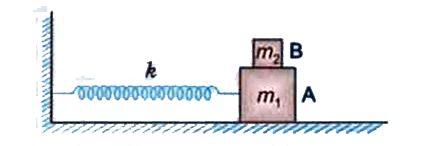
View SolutionA block A of mass m1 is placed on a horizontal frictionless table. It is connected to one end of a light spring of force constant k whose other end is fixed to a wall. A small block B of mass m2 is placed on block A. The coefficient of static friction between the blocks is μ. The system is displaced slightly from its equilibrium position and released. What is the maximum amplitude of the resulting simple harmonic motion of the system so that the upper block does not slip over the lower block ?
View Solution
