कथन-1: α तथा β के सभी मानों के लिए, बिन्दुओं B(ccosα,csinα) और C(ccosβ,csinβ) को जोड़ने वाली रेखा के बिन्दु (1,1) से BC पर लम्ब समद्विभाजित करता है
कथन-2: शीर्ष से डाला गया लम्ब एक समद्विबाहु त्रिभुज के आधार को समद्विभाजित करता है।
कथन-1 सही है, कथन-2 सही है, कथन-1 के लिए, कथन-2 का स्पष्टीकरण सही है
कथन -1 सही है, कथन -2 सही है, कथन-1 के लिए, कथन-2 का स्पष्टीकरण सही नहीं है
कथन-1 सही है, कथन-2 गलत है
कथन-1 गलत है, कथन-2 सही है
The correct Answer is:D
Step by step video, text & image solution for कथन-1: alpha तथा beta के सभी मानों के लिए, बिन्दुओं B (c cos alpha , c sin alpha ) और C ( c cos beta, c sin beta) को जोड़ने वाली रेखा के बिन्दु (1,1) से BC पर लम्ब समद्विभाजित करता है कथन-2: शीर्ष से डाला गया लम्ब एक समद्विबाहु त्रिभुज के आधार को समद्विभाजित करता है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - सरल रेखा EXERCISE - JEE ADVANCE (Comprehension type questions)9videos
सरल रेखा
- BOOK - ERRORLESS HINDICHAPTER - सरल रेखा EXERCISE - JEE ADVANCE (Matrix Match type questions)4videos
सरल रेखा
- BOOK - ERRORLESS HINDICHAPTER - सरल रेखा EXERCISE - JEE ADVANCE (More than one correct answer)6videos
सरल रेखा
- BOOK - ERRORLESS HINDICHAPTER - सम्मिश्र संख्यायेंEXERCISE - Jee Advanced (Integer)9videos
सम्मिश्र संख्यायें
- BOOK - ERRORLESS HINDICHAPTER - सारणिक तथा आव्यूह EXERCISE - JEE ADVANCED MORE THAN ONE CORRECT ANSWERS (Matrix Match type questions)4videos
सारणिक तथा आव्यूह
Similar Questions
माना उस स्थिति में जब अक्षे कोण 'ω' पर झुकी हुई है यदि एक बिन्दु P के निर्देशांक (x1,y1) है , तब PN=x1,PM=y1 जहाँ PM , y -अक्ष के समान्तर है और PN ,x -अक्ष के समान्तर है P से जाने वाली सरल रेखा का समीकरण और x -अक्ष के साथ θ कोण बनाए RQ=y−y1,PQ=x−x1 है
ΔPQR से
PQsin(ω−θ)=PQsinθ
y−y1=sinθsin(ω−θ)(x−x1)
y−y1=m(x−x1)के रूप में लिखने पर जहाँ, m=sinθsin(ω−θ)
∴ यदि रेखा का ढाल m है , तब रेखा का x -अक्ष से झुकाव कोण
tanθ=(msinω1+mcosω) दिया जाता है
उपरोक्त धारणा को पढ़कर निम्नलिखित प्रश्नो के उत्तर दो।
अक्षे 60∘ के कोण पर झुकी हुई है , तब सरल रेखा y=2x+5 का x अक्ष के साथ झुकाव है01:02View Solution
02:47View Solutionबिन्दुओं (1, 3), (5,0) तथा (-1, 2) से निर्मित त्रिभुज के अंदर स्थित सभी बिन्दु निम्न में से कौन से प्रतिबंध संतुष्ट करेंगे
09:56View Solutionमान लीजिए कि z कोई सम्मिश्र संख्या है जिसके लिये |z−3−2i|≤2 सत्य है, तो |2z-6+5i| का न्यूनतम मान है
06:05View Solutionइस खण्ड में कुछ प्रश्न है। प्रत्येक प्रश्न में कॉलम -I में कुछ कथन (A,B, C और D) और कॉलम -II में कुछ कथन (p,q,r,s और t ) है। कॉलम -I का कोई भी कथन कॉलम -II के एक कथन या एक से अधिक कथनो से मेल खाता है। उदाहरण के लिए दिए हुए प्रश्न में यदि कथन B कथनो q और r से मेल खाता है, तो ORS में उस प्रश्न के लिये कथन B के सामने q और r से संबंधित बुलबुलो को काला कीजिए।
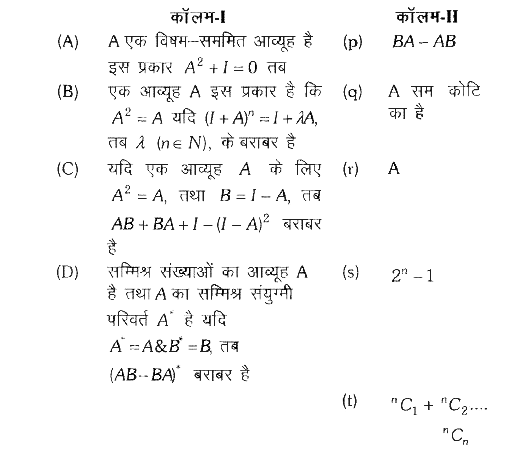05:32View SolutionIf cot(α+β)=0, then sin(α+2β) can be (a)−sinα (b) sinβ (c) cosα (d) cosβ
03:06View SolutionIf alpha=cos alpha+i sin alpha,b=cos beta+i sin beta,c=cos gamma+i sin gamma and (b)/(c)+(c)/(a)+(a)/(b)=1 then cos(beta-gamma)+cos(gamma-alpha)+cos(alpha-beta)=
04:32View Solutionमूलबिंदु से बिन्दुओ (acosα,asinα) तथा (acosβ,asinβ) को मिलाने वाली रेखा डाले गये लम्ब कि लम्बाई ज्ञात कीजिए ।
04:15View Solutionसदिशों ¯a+¯b असंरेखी सदिशों ¯a और ¯b के बीच के कोण को समद्विभाजित करता है, यदि ...........
02:38View Solutionसदिश ¯a=α¯i+2¯j+β¯k, सदिशों ¯b=¯i+¯j तथा ¯c=¯j+¯k के तल में स्थित है तथा ¯b और ¯c के बीच के कोण का समद्विभाजन करता है, तो निम्न में से कौनसा α और β के सम्भावित मान प्रदान करता है ?
02:38View Solutionउन त्रिभुजों के क्षेत्रफल ज्ञात कीजिए जिनके शीर्ष निम्नलिखित है :
(0,0)(acosα,bsinα) और (acosβ,bsinβ)02:55View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
03:47View Solutionयदि समीकरण ax2+bx+c=0 के मूल α व βहै तब αaβ+b+βaα+b बराबर है
03:47View Solutionउस बिन्दु के निर्देशांक ज्ञात कीजिए जो बिन्दुओं (3, 7) और (−1,−5) को मिलाने वाली रेखा को 2:3 के अनुपात में अन्तः विभाजित करता है।
04:02View Solutionउस बिन्दु के निर्देशांक ज्ञात कीजिए जो बिन्दुओं (3, 7) और (−1,−5) को मिलाने वाली रेखा को 2:3 के अनुपात में अन्तः विभाजित करता है।
View Solutionउस बिन्दु के निर्देशांक ज्ञात कीजिए, जो बिन्दुओं (4,-3) तथा (8,5) को मिलाने वाली रेखा को 3:1 में बाह्यतः विभाजित करता है।
05:24View Solution