रेखा L1: y-x = 0 औरL2 : 2x + y = 0, क्रमशः P और Q पर रेखा L3.::y+ 2 = 0 को प्रतिच्छेद करती है।L1 और L2 के बीच के न्यूनकोण का अर्धक, R पर L3 को प्रतिच्छेद करता है।
कथन-1: माना S1::x2+y2−10x−12y−39=0
S2:x2+y2−2x−4y+1=0 और
S3:2x2+2y2−20x−24y+78=0 इन वृत्तों के मूल केन्द्रों को जोड़े में लिया जाता है। वह (-2,-3) है।
कथन-2: तीन वृत्तों के तीन मूल अक्षों के प्रतिच्छेद बिन्दु जोड़े में लिए जाते हैं, तब इन्हें मूल केन्द्र कहते हैं।
कथन-1 सही है, कथन-2 सही है, कथन-1 के लिए, कथन-2 का स्पष्टीकरण सही है
कथन -1 सही है, कथन -2 सही है, कथन-1 के लिए, कथन-2 का स्पष्टीकरण सही नहीं है
कथन-1 सही है, कथन-2 गलत है
कथन-1 गलत है, कथन-2 सही है
The correct Answer is:D
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - सरल रेखा EXERCISE - JEE ADVANCE (Comprehension type questions)9videos
सरल रेखा
- BOOK - ERRORLESS HINDICHAPTER - सरल रेखा EXERCISE - JEE ADVANCE (Matrix Match type questions)4videos
सरल रेखा
- BOOK - ERRORLESS HINDICHAPTER - सरल रेखा EXERCISE - JEE ADVANCE (More than one correct answer)6videos
सरल रेखा
- BOOK - ERRORLESS HINDICHAPTER - सम्मिश्र संख्यायेंEXERCISE - Jee Advanced (Integer)9videos
सम्मिश्र संख्यायें
- BOOK - ERRORLESS HINDICHAPTER - सारणिक तथा आव्यूह EXERCISE - JEE ADVANCED MORE THAN ONE CORRECT ANSWERS (Matrix Match type questions)4videos
सारणिक तथा आव्यूह
Similar Questions
माना उस स्थिति में जब अक्षे कोण 'ω' पर झुकी हुई है यदि एक बिन्दु P के निर्देशांक (x1,y1) है , तब PN=x1,PM=y1 जहाँ PM , y -अक्ष के समान्तर है और PN ,x -अक्ष के समान्तर है P से जाने वाली सरल रेखा का समीकरण और x -अक्ष के साथ θ कोण बनाए RQ=y−y1,PQ=x−x1 है
ΔPQR से
PQsin(ω−θ)=PQsinθ
y−y1=sinθsin(ω−θ)(x−x1)
y−y1=m(x−x1)के रूप में लिखने पर जहाँ, m=sinθsin(ω−θ)
∴ यदि रेखा का ढाल m है , तब रेखा का x -अक्ष से झुकाव कोण
tanθ=(msinω1+mcosω) दिया जाता है
उपरोक्त धारणा को पढ़कर निम्नलिखित प्रश्नो के उत्तर दो।
अक्षे 60∘ के कोण पर झुकी हुई है , तब सरल रेखा y=2x+5 का x अक्ष के साथ झुकाव है03:09View Solution
04:01View Solutionबिन्दुओं (1, 3), (5,0) तथा (-1, 2) से निर्मित त्रिभुज के अंदर स्थित सभी बिन्दु निम्न में से कौन से प्रतिबंध संतुष्ट करेंगे
08:43View Solutionमान लीजिए कि z कोई सम्मिश्र संख्या है जिसके लिये |z−3−2i|≤2 सत्य है, तो |2z-6+5i| का न्यूनतम मान है
04:23View Solutionइस खण्ड में कुछ प्रश्न है। प्रत्येक प्रश्न में कॉलम -I में कुछ कथन (A,B, C और D) और कॉलम -II में कुछ कथन (p,q,r,s और t ) है। कॉलम -I का कोई भी कथन कॉलम -II के एक कथन या एक से अधिक कथनो से मेल खाता है। उदाहरण के लिए दिए हुए प्रश्न में यदि कथन B कथनो q और r से मेल खाता है, तो ORS में उस प्रश्न के लिये कथन B के सामने q और r से संबंधित बुलबुलो को काला कीजिए।
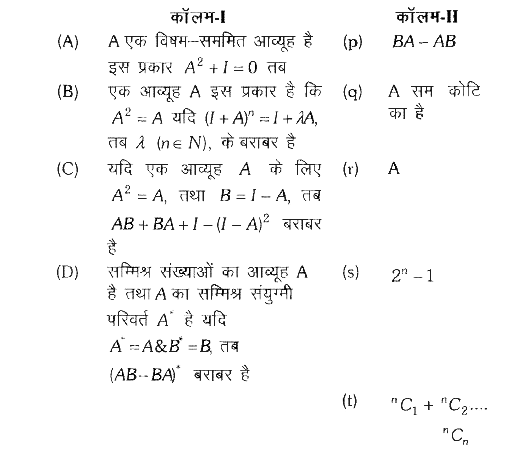
04:43View SolutionThe circle x2+y2−4x−2y=11 makes equal intercepts on the lines L1:x+2y+1=0 and L2. Then equation of L2 cannot be 2x+y+1=0 2x−y+3=0 2x+y=0 (d) 3x−2y+2=0
02:55View SolutionThe combined equation of the lines L1 and L2 is 2x2+6xy+y2=0 and that lines L3 and L4 is 4x2+18xy+y2=0. If the angle between L1 and L4 be α, then the angle between L2 and L3 will be
01:48View SolutionL1:x+1−3=y−32=z+21,L2:x1=y−7−3=z+72
The lines L1 and L2 are -05:00View SolutionL1:x+1−3=y−32=z+21,L2:x1=y−7−3=z+72
The lines L1 and L2 intersect at the point10:33View SolutionL1:x+1−3=y−32=z+21,L2:x1=y−7−3=z+72
Equation of plane containinng L1 and L2 is -View SolutionEquation of the circumcircle of a triangle formed by the lines L1=0,L2=0andL3=0 can be written as L1L2+λL2L3+μL3L1=0, where λandμ are such that coefficient of x2 =coefficient of y2 and coefficient of xy=0.
L1L22+λL2L23+μL21=0 represents03:34View SolutionEquation of the circumcircle of a triangle formed by the lines L1=0,L2=0andL3=0 can be written as L1L2+λL2L3+μL3L1=0, where λandμ are such that coefficient of x2 =coefficient of y2 and coefficient of xy=0.
If L1L2+λL2L3+μL3L1=0 is such that μ=0andλ is non-zero, then it represents07:05View Solutionवृत्त x2+y2−2x−4y+3=0 का बिन्दु (2,3) पर अभिलम्ब वृत्त x2+y2=1 को बिन्दु P और Q पर प्रतिच्छेद करता है। व्यास PQ वाले वृत्त का क्षेत्रफल है
02:19View Solutionयदि समतलों 2x−2y+3z−2=0,x−y+z+1=0, की परिच्छेदी रेखा L1 है तथा समतलों x+2y−z−3=0,3x−y+2z−1=0 की परिच्छेदी रेखा L2 है तो मूल बिंदू की दूरी उस समतल से जो रेखाओं L1 और L2 का अंतर्विष्ट करता है:
(i) 12√2 (ii) 1√2 (iii) 14√2 (iv) 13√202:11View SolutionL1:2(x−1)+3(y+2)+(z−7)=0 and L1:2(x+1)−3(y+2)+(z+7)=0 are two planes.
05:14View SolutionConsider the lines L1≡3x−4y+2=0 and L2≡3y−4x−5=0. Now, choose the correct statement(s).
(a)The line x+y=0 bisects the acute angle between L1and L2 containing the origin.
(b)The line x-y+1=0 bisects the obtuse angle between L1 and L2 not containing the origin.
(c)The line x+y+3=0 bisects the obtuse angle between L1 and L2 containing the origin.
(d)The line x-y+1=0 bisects the acute angle between L1 and L2 not containing the origin.03:27View Solution