A rocket is going upward with acceleration motion. A man string in it feels his weight increased 5 time his own weight. If the mass of the rocket including that of the man is 1.0×104kg , how much force is being applied by rocket engine? (Takeg=10ms−2) .
1.5×104N
2. 5×105N
3. 5×108N
4. 2×104N
The correct Answer is:B
To solve the problem, we need to find the force being applied by the rocket engine. Let's break it down step by step.
Step 1: Understand the Problem
The rocket is accelerating upwards, and the man inside feels his weight increased to 5 times his own weight. We need to calculate the force exerted by the rocket engine.
Step 2: Define Variables
- Let the mass of the rocket including the man be m=1.0×104kg.
- The acceleration due to gravity is g=10m/s2.
- The increased weight felt by the man is 5×weight of the man.
Step 3: Calculate the Weight of the Man
The weight of the man can be expressed as:
W=mg
Since the total mass of the rocket including the man is given, we can express the total weight as:
Wtotal=mg=(1.0×104kg)×(10m/s2)=1.0×105N
Step 4: Set Up the Equation
When the rocket accelerates upwards, the man feels an effective weight that is 5 times his actual weight. The effective weight can be expressed as:
Weffective=5mg
This means:
Weffective=5×(mg)
Step 5: Relate Forces
The net force acting on the man when the rocket accelerates upwards can be expressed as:
Fnet=ma+mg
Where a is the acceleration of the rocket. Since the effective weight is 5 times the actual weight:
ma+mg=5mg
Step 6: Solve for Acceleration
Rearranging the equation gives:
ma=5mg−mg
ma=4mg
Dividing both sides by m:
a=4g
Substituting g=10m/s2:
a=4×10=40m/s2
Step 7: Calculate the Force Exerted by the Rocket Engine
The total force exerted by the rocket engine can be calculated using Newton's second law:
F=m(a+g)
Substituting the values:
F=(1.0×104kg)×(40m/s2+10m/s2)
F=(1.0×104kg)×(50m/s2)
F=5.0×105N
Final Answer
The force being applied by the rocket engine is:
F=5.0×105N
---
The rocket is accelerating upwards, and the man inside feels his weight increased to 5 times his own weight. We need to calculate the force exerted by the rocket engine.
- Let the mass of the rocket including the man be m=1.0×104kg.
- The acceleration due to gravity is g=10m/s2.
- The increased weight felt by the man is 5×weight of the man.
The weight of the man can be expressed as:
W=mg
Since the total mass of the rocket including the man is given, we can express the total weight as:
Wtotal=mg=(1.0×104kg)×(10m/s2)=1.0×105N
When the rocket accelerates upwards, the man feels an effective weight that is 5 times his actual weight. The effective weight can be expressed as:
Weffective=5mg
This means:
Weffective=5×(mg)
The net force acting on the man when the rocket accelerates upwards can be expressed as:
Fnet=ma+mg
Where a is the acceleration of the rocket. Since the effective weight is 5 times the actual weight:
ma+mg=5mg
Rearranging the equation gives:
ma=5mg−mg
ma=4mg
Dividing both sides by m:
a=4g
Substituting g=10m/s2:
a=4×10=40m/s2
The total force exerted by the rocket engine can be calculated using Newton's second law:
F=m(a+g)
Substituting the values:
F=(1.0×104kg)×(40m/s2+10m/s2)
F=(1.0×104kg)×(50m/s2)
F=5.0×105N
The force being applied by the rocket engine is:
F=5.0×105N
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - HOTS
8 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Exemplar Problems
9 Videos
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT Exemplar
5 Videos
Similar Questions
A rocket burns 50g of fuel per second ejecting it as a gas with a velocity of 5×10cms−1. What force is exerted by the gas on the rocket?
View SolutionWith what force must a man pull on the rope to hold the plank in position it the man weights 60 kg? Neglect the weight of the plank, rope and pulley ( Take g= 10m/s2)

View Solution
Knowledge Check
The person o( mass 50 kg slands on a weighing scale on a lift. If the lift is ascending upwards with a uniform acceleration of 9ms−2, what would be the reading of the weighting scale? (Take g=10ms−2)
A50kgB60kgC96kgD176kgTwo blocks A and B of masses 10 kg and 15 kg are placed in contact with each other rest on a rough horizontal surface as shown in the figure. The coefficient of friction between the blocks and surface is 0.2. A horizontal force of 200 N is applied to block A. The acceleration of the system is (Take g=10ms−2)
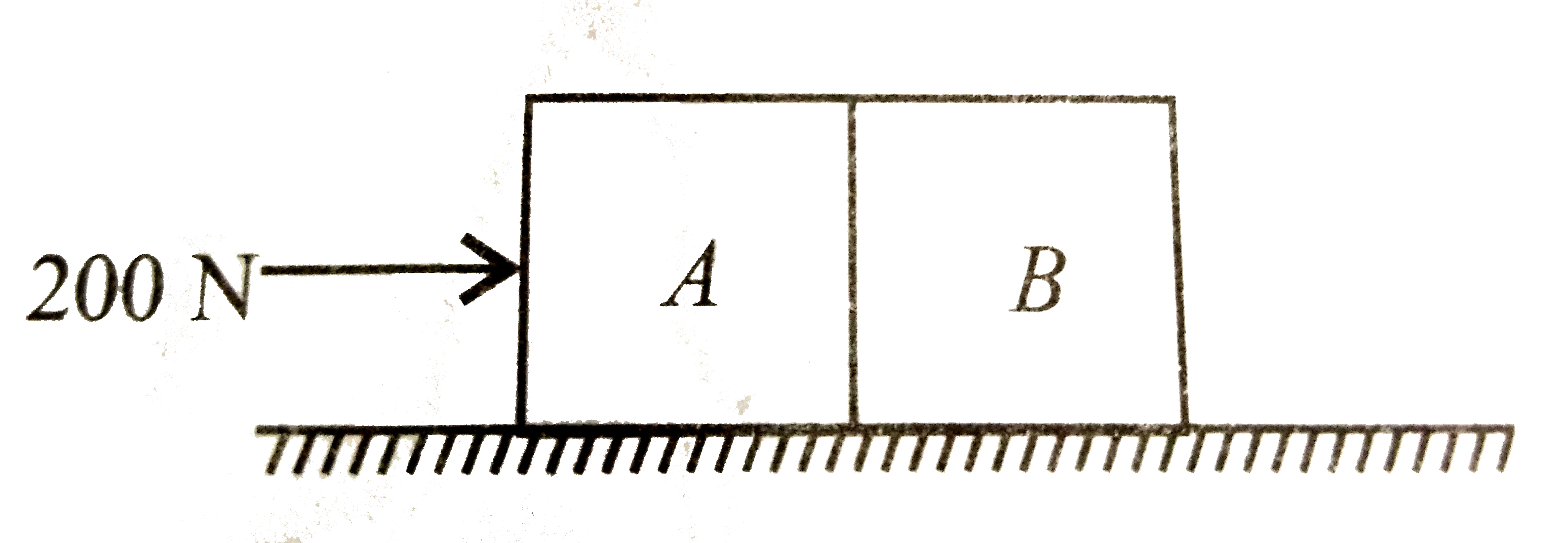 A4ms−2B6ms−2C8ms−2D10ms−2
A4ms−2B6ms−2C8ms−2D10ms−2
A rocket with a lift-off mass 3.5×104kg is blasted upwards with an initial acceleration of 10m/s2. Then the initial thrust of the blast is
View SolutionA rocket with a lift-off mass 3.5×104kg is blasted upwards with an initial acceleration of 10m/s2. Then the initial thrust of the blast is
View SolutionA rocket with a lift-off mass 3.5×104kg is blasted upwards with an initial acceleration of 10m/s2. Then the initial thrust of the blast is
View SolutionA man of 60kg mass is in a lift. Find the apparent weight of the man when the lift is moving up with uniform speed(g=10ms−2)
View SolutionIf the elevator in shown figure is moving upwards with constant acceleration 1ms−2, tension in the string connected to block A of mass 6 kg would be ( take, g=10ms−2)
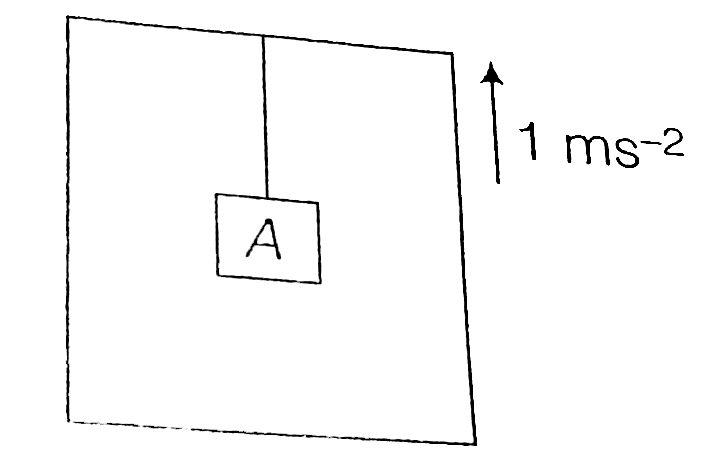
View SolutionA wooden block of mass 1kg and density 800Kgm−3 is held stationery, with the help of a string, in a container filled with water of density 1000kgm−3 as shown in the figure. If the container is moved upwards with an acceleration of 2ms−2, then the tension in the string will be ( takeg=10ms−2)
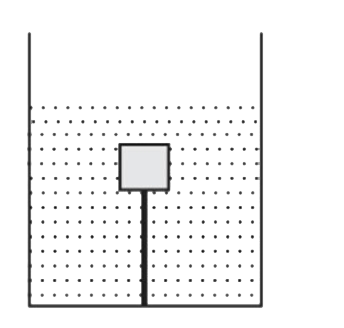
View Solution
