The coefficient of static friction between the box and the train's floor is 0.2. The maximum acceleration of the train in which a box lying on its floor will remain stationary is (Take g=10ms−2)
2ms−2
4ms−2
6ms−2
8ms−2
The correct Answer is:D
To find the maximum acceleration of the train such that the box remains stationary on its floor, we can follow these steps:
Step 1: Understand the Forces Acting on the Box
When the train accelerates, a pseudo force acts on the box in the opposite direction of the train's acceleration. The forces acting on the box are:
- Weight (mg) acting downwards.
- Normal force (N) acting upwards.
- Frictional force (f_s) acting in the direction of the train's acceleration.
Step 2: Write the Equations for Forces
For the box to remain stationary relative to the train, the static frictional force must balance the pseudo force due to the train's acceleration. Thus, we can write:
- The normal force (N) is equal to the weight of the box: N=mg.
- The pseudo force acting on the box due to the train's acceleration (a) is given by: fpseudo=ma.
Step 3: Apply the Static Friction Condition
The maximum static frictional force can be expressed as:
fs≤μsN
Substituting for N, we get:
fs≤μsmg
Step 4: Set Up the Equation
Since the box is stationary, the static frictional force must equal the pseudo force:
ma≤μsmg
Step 5: Cancel Mass (m)
Since mass (m) appears on both sides of the equation, we can cancel it out:
a≤μsg
Step 6: Substitute the Values
We know:
- Coefficient of static friction (μs) = 0.2
- Acceleration due to gravity (g) = 10 m/s²
Substituting these values into the equation gives:
a≤0.2×10
Step 7: Calculate Maximum Acceleration
Calculating this gives:
a≤2m/s2
Conclusion
Thus, the maximum acceleration of the train in which the box will remain stationary is:
Maximum Acceleration=2m/s2
---
When the train accelerates, a pseudo force acts on the box in the opposite direction of the train's acceleration. The forces acting on the box are:
- Weight (mg) acting downwards.
- Normal force (N) acting upwards.
- Frictional force (f_s) acting in the direction of the train's acceleration.
For the box to remain stationary relative to the train, the static frictional force must balance the pseudo force due to the train's acceleration. Thus, we can write:
- The normal force (N) is equal to the weight of the box: N=mg.
- The pseudo force acting on the box due to the train's acceleration (a) is given by: fpseudo=ma.
The maximum static frictional force can be expressed as:
fs≤μsN
Substituting for N, we get:
fs≤μsmg
Since the box is stationary, the static frictional force must equal the pseudo force:
ma≤μsmg
Since mass (m) appears on both sides of the equation, we can cancel it out:
a≤μsg
We know:
- Coefficient of static friction (μs) = 0.2
- Acceleration due to gravity (g) = 10 m/s²
a≤0.2×10
Calculating this gives:
a≤2m/s2
Thus, the maximum acceleration of the train in which the box will remain stationary is:
Maximum Acceleration=2m/s2
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - HOTS
8 Videos
- LAWS OF MOTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Exemplar Problems
9 Videos
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT Exemplar
5 Videos
Similar Questions
Knowledge Check
The coefficient of static friction between a box and a ramp is 0.5. The ramp's incline angle is 30∘. If the box is placed at rest on the ramp, the box will
Aaccelerate down the rampBaccelerate briefly down the ramp but then slow down and stopCmove with constant velocity down the rampDnot moveThe coefficient of friction between the tyres and the road is 0.1. The maximum speed with which a cyclist can take a circular turn of radius 3 m without skidding is (Take g=10ms−2)
A√15ms−1B√3ms−1C√30ms−1D√10ms−1
If the coefficient of friction between A and B is μ, the maximum acceleration of the wedge A for which B will remain at rest with respect to the wedge is

View SolutionFigure shows a man standing stationary with respect to a horizontal conveyor belt that is accelerating with l1ms−2 . The net force on the man, if the coefficient of static friction between the man's shoes and the belt is 0.2, up to what acceleration of the belt can the man continue to be stationary relative to the belt
 (mass of the man-65kg)
(mass of the man-65kg)
View SolutionA block of mass 10 kg is kept on a rough inclined plane as shown in the figure. A force of 3 N is applied on the block. The coefficient of static friction between the plane and the block is 0.6 What should be the minimum value of force P, such that the block doesnot move downward? (take g=10ms−2)

View SolutionA block of mass 10 kg is kept on a rough inclined plane as shown in the figure. A force of 3 N is applied on the block. The coefficient of static friction between the plane and the block is 0.6 What should be the minimum value of force P, such that the block doesnot move downward? (take g=10ms−2)

View SolutionA block of mass 5kg is (i) pushed in case (A) and (ii) pulled in case (B), by a force F=20N, making an angle of 30∘ with the horizontal, as shown in the figures. The coefficient of friction between the block and floor is μ=0.2. The difference between the accelerattion of the block, in case (B) and case (A) will be : (g=10ms−2).
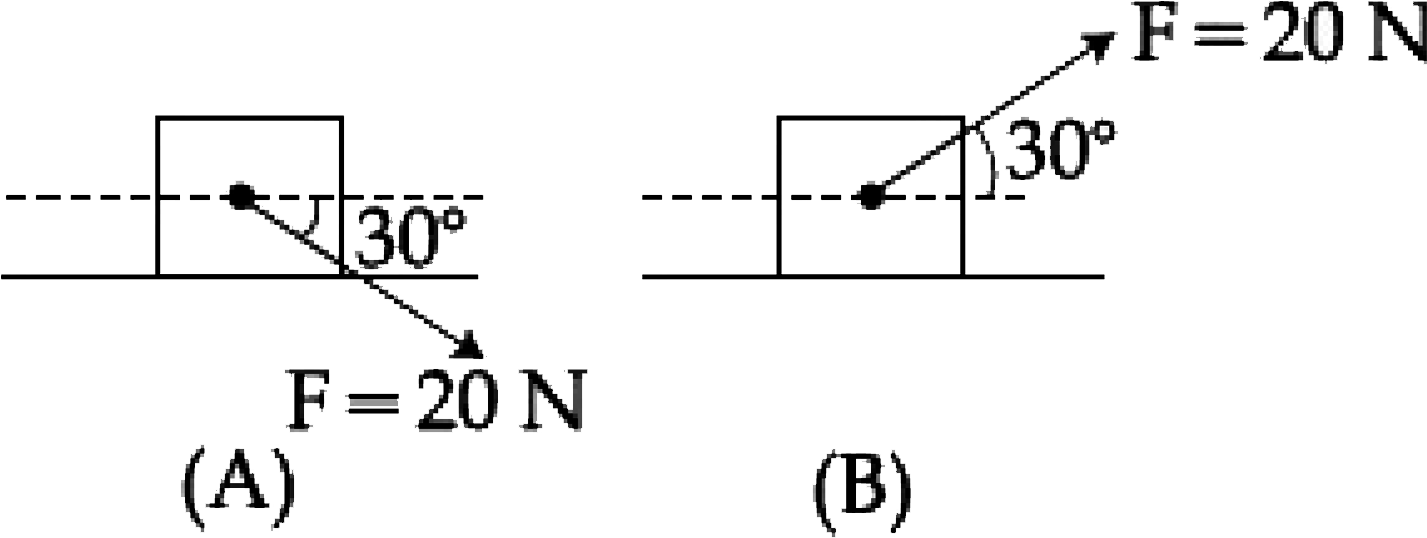 .
.
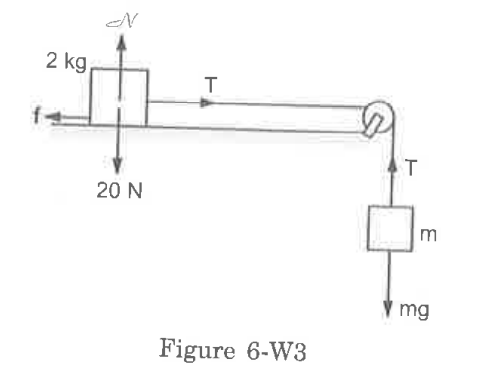
View SolutionThe coefficient of static friction between the block of 2 kg and the table shown in figurwe is μs=0.2 What should be the maximum value of m so tht the blocks do not move? Take g=10ms2. The string and the pulley are light and smooth.
View Solution
