A particle in a certain conservative force field has a potential energy given by V=20xyz. The force exerted on it is
(20yz)ˆi+(20xz)ˆj+(20xyz2)ˆk
−(20yz)ˆi−(20xz)ˆj+(20xyz2)ˆk
−(20yz)ˆi−(20xz)ˆj−(20xyz2)ˆk
(20yz)ˆi+(20xz)ˆj−(20xyz2)ˆk
The correct Answer is:B
To find the force exerted on a particle in a conservative force field with a given potential energy, we can use the relationship between force and potential energy. The force F is related to the potential energy V by the equation:
F=−∇V
Where ∇V is the gradient of the potential energy. The gradient in three dimensions is given by:
∇V=(∂V∂x,∂V∂y,∂V∂z)
Given the potential energy function:
V=20xyz
We will calculate the partial derivatives with respect to x, y, and z.
Step 1: Calculate ∂V∂x
∂V∂x=∂∂x(20xyz)=20yz
Step 2: Calculate ∂V∂y
∂V∂y=∂∂y(20xyz)=20xz
Step 3: Calculate ∂V∂z
Using the quotient rule for differentiation:
∂V∂z=∂∂z(20xyz)=−20xyz2
Step 4: Combine the results to find the force
Now we can express the force vector:
F=−∇V=−(20yz,20xz,−20xyz2)
This simplifies to:
F=(−20yz,−20xz,20xyz2)
Final Answer
Thus, the force exerted on the particle is:
F=−20yz^i−20xz^j+20xyz2^k
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - NCERT18videos
WORK , ENERGY AND POWER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - ASSERTION & REASON15videos
WORK , ENERGY AND POWER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - Assertion And Reason15videos
WAVES
Similar Questions
A particle moves in one dimension in a conservation force field. The potential energy is depicted in the graph below.
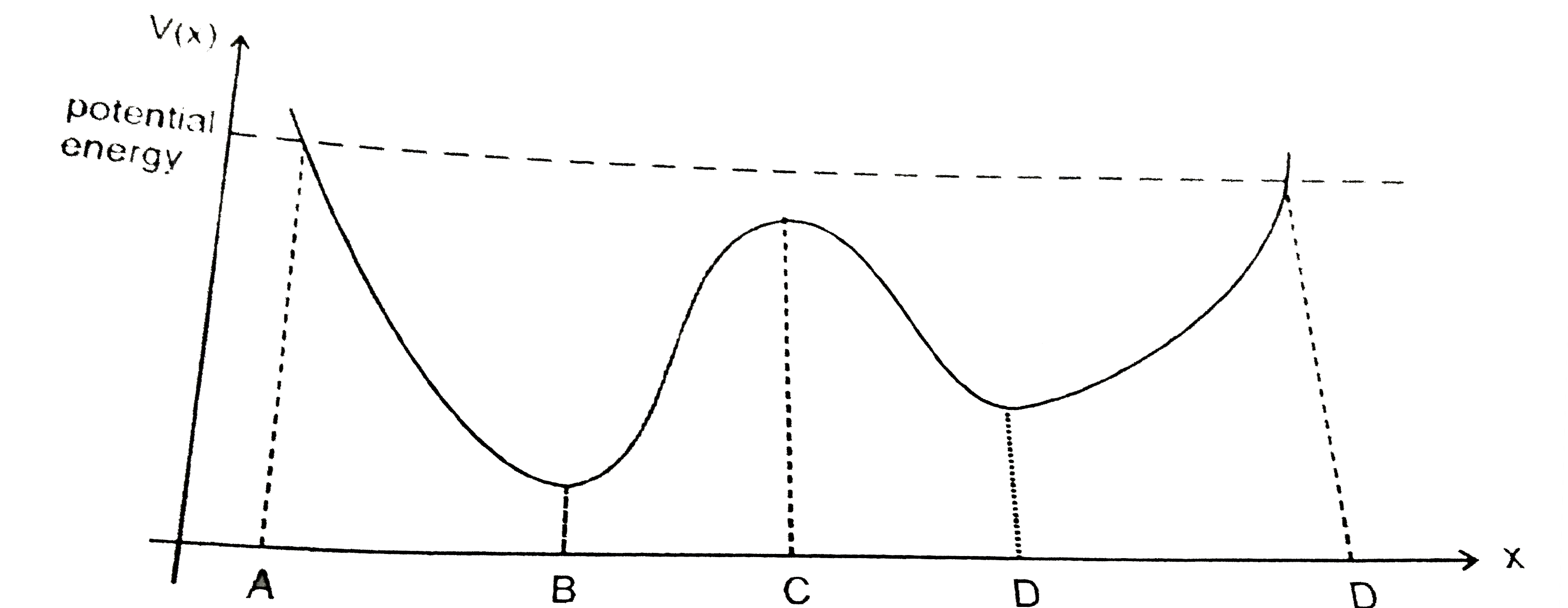
If the particle starts to move from rest from the point A, thenView SolutionA particle moves in one dimension in a conservation force field. The potential energy is depicted in the graph below.

If the particle starts to move from rest from the point A, thenView SolutionThe potential energy ‘V’ of a particle moving along the positive x-direction in a conservative force field varies as shown in the figure. The total energy is E=2. Draw the corresponding kinetic energy K vs x graph.
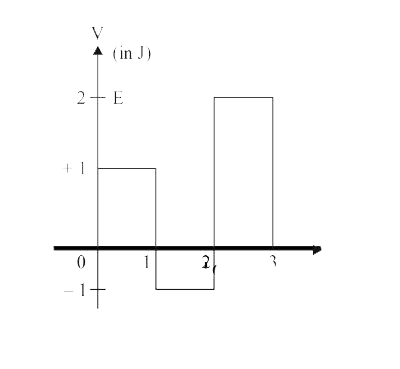 View Solution
View SolutionA particle of mass m=3 kg is moving on a straight line in a conservative force field in which the potential energy associated with the particle is given by U(y)=2y2−30y+450. At t=0, particle is at y=8m and moving towards positive y- axis with 1m/s
View SolutionA particle is moving in a conservative force field from point A to point B.UA and UB are the potential energies of the particle at point A and B and WC is the work done by conservative forces in the process of taking the particle from A and B, which of the following is true?
View SolutionA particle is executing simple harmonic motion in a conservative force field. The total energy of simple harmonic motion is given by E=ax2+bv2where ‘x’ is the displacement from mean position x = 0 and v is the velocity of the particle at x then choose the INCORRECT statements.{Potential energy at mean position is assumed to be zero}
View SolutionAs a particle moves along the x−axis, it is acted upon by a conservative force. The potential energy is shown below as a function of the coordinate x of the particle. Rank the labelled regions accoeording to the magnitude of force, least to greatest.
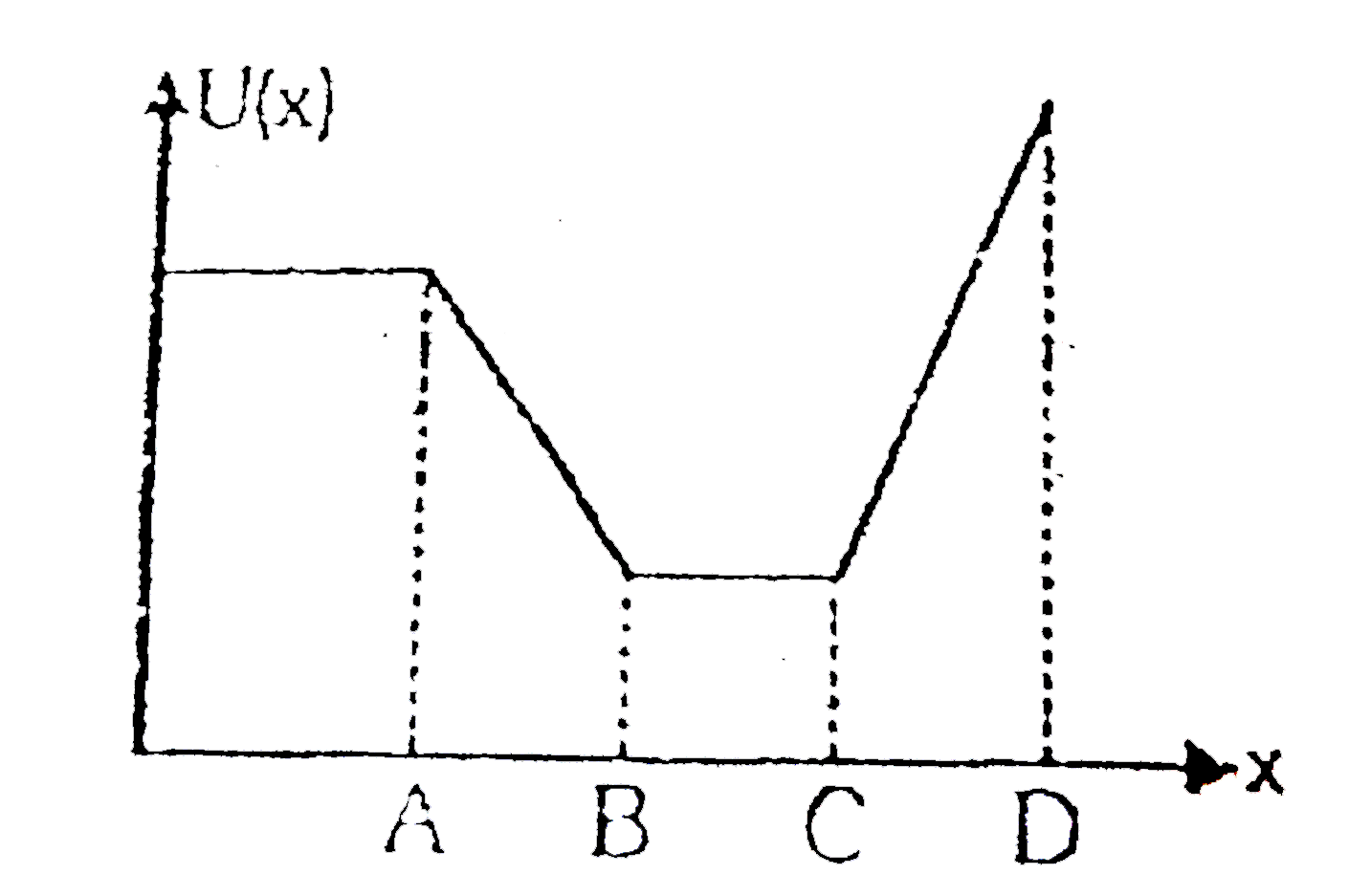 View Solution
View SolutionA particle slides on frictionless x - y plane. It is acted on by a conservative force described by the potential - energy function U(x,y)=12k(x2+y2). Derive an expression for the force acting on the particle.
View SolutionAn α particle is situated in an electric field of 106N/C. The force exerted or it is
View SolutionA single conservative force F(x) acts on a 1.0−kg particle that moves along the x-axis. The potential energy U(x) is given by U(x)=20+(x−2)2 where x is in meters. At x=5.0m, the particle has a kinetic energy of 20J.
What is the mechanical energy of a system?View Solution

