A particle slides on frictionless x - y plane. It is acted on by a conservative force described by the potential - energy function U(x,y)=12k(x2+y2). Derive an expression for the force acting on the particle.
To derive the expression for the force acting on a particle in a conservative force field described by the potential energy function U(x,y)=12k(x2+y2), we will follow these steps:
Step 1: Understand the relationship between force and potential energy
The force →F acting on a particle in a conservative field can be derived from the potential energy function U using the formula:
→F=−∇U
where ∇U is the gradient of the potential energy function.
Step 2: Calculate the gradient of U
The gradient in two dimensions is given by:
∇U=(∂U∂x,∂U∂y)
We will calculate the partial derivatives of U with respect to x and y.
Step 3: Compute ∂U∂x
Given:
U(x,y)=12k(x2+y2)
Differentiating U with respect to x:
∂U∂x=12k⋅2x=kx
Step 4: Compute ∂U∂y
Now, differentiating U with respect to y:
∂U∂y=12k⋅2y=ky
Step 5: Write the gradient vector
Now we can write the gradient vector:
∇U=(kx,ky)
Step 6: Find the force vector
Using the relationship →F=−∇U:
→F=−(kx,ky)=(−kx,−ky)
Step 7: Express the force in vector form
We can express the force vector in terms of unit vectors ^i and ^j:
→F=−kx^i−ky^j
Step 8: Introduce the position vector
The position vector →r can be defined as:
→r=x^i+y^j
Thus, we can express the force in terms of the position vector:
→F=−k→r
Final Expression
The final expression for the force acting on the particle is:
→F=−k→r
This indicates that the force is directed towards the origin and is proportional to the position vector.
---
The force →F acting on a particle in a conservative field can be derived from the potential energy function U using the formula:
→F=−∇U
where ∇U is the gradient of the potential energy function.
The gradient in two dimensions is given by:
∇U=(∂U∂x,∂U∂y)
We will calculate the partial derivatives of U with respect to x and y.
Given:
U(x,y)=12k(x2+y2)
Differentiating U with respect to x:
∂U∂x=12k⋅2x=kx
Now, differentiating U with respect to y:
∂U∂y=12k⋅2y=ky
Now we can write the gradient vector:
∇U=(kx,ky)
Using the relationship →F=−∇U:
→F=−(kx,ky)=(−kx,−ky)
We can express the force vector in terms of unit vectors ^i and ^j:
→F=−kx^i−ky^j
The position vector →r can be defined as:
→r=x^i+y^j
Thus, we can express the force in terms of the position vector:
→F=−k→r
The final expression for the force acting on the particle is:
→F=−k→r
This indicates that the force is directed towards the origin and is proportional to the position vector.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION2videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - TRY YOURSELF95videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))12videos
WAVES
Similar Questions
A particle is moving on frictionless XY-plane. It is acted on by a conservative force described by the potential-energy function.
U(x,y,z)=12k(x2+y2+z2)
where , k=constant
Derive an expression for the force an the particle.View SolutionAs a particle moves along the x−axis, it is acted upon by a conservative force. The potential energy is shown below as a function of the coordinate x of the particle. Rank the labelled regions accoeording to the magnitude of force, least to greatest.
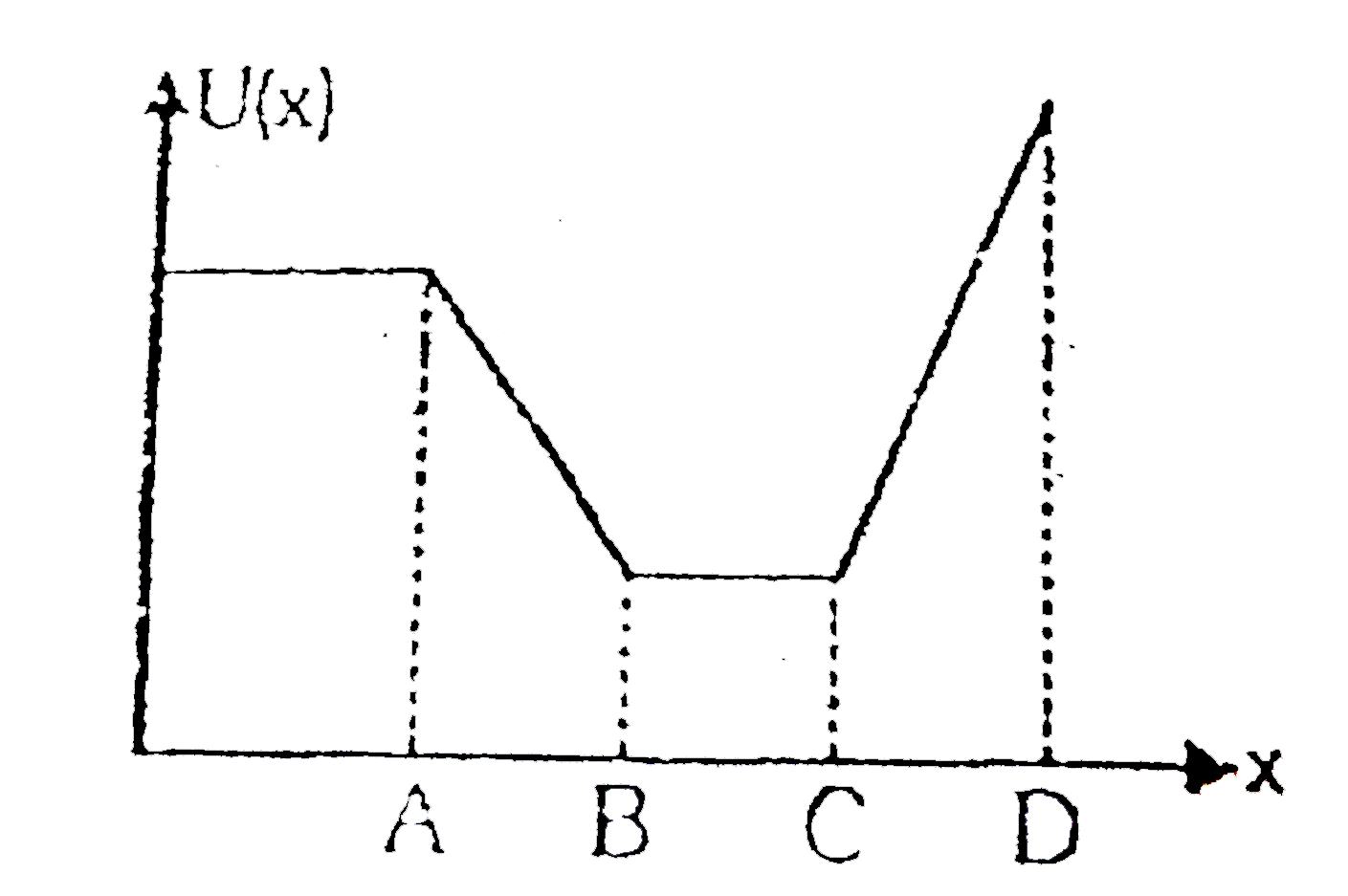 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The motion of a particle of mass m is described by y=ut+12gt2 . Find the force acting on the particale .
AmgBμtC2mgD2μt
The potential energy of a body is given by U=A−Bx2 (where x is the displacement). The magnitude of force acting on the partical is
View SolutionThe motion of a particle of mass m is described by y=ut+12gt2 . Find the force acting on the particale .
View SolutionThe potential energy of a force filed →F is given by U(x,y)=sin(x+y). The force acting on the particle of mass m at (0,π4) is
View SolutionFigure shows a plot of potential energy function U(x)=kx2 where x=displacement and k=constant. Identify the correct conservative force function F(x)
 View Solution
View SolutionA particle free to move along x-axis is acted upon by a force F=−ax+bx2whrteaandbarepositiveconstants., the correct variation of potential energy function U(x) is best represented by.
View SolutionA potential energy function for a two-dimensional force is the form U=3x2y−7x. Find the force that acts at the point (x,y).
View SolutionA particle of mass m=3 kg is moving on a straight line in a conservative force field in which the potential energy associated with the particle is given by U(y)=2y2−30y+450. At t=0, particle is at y=8m and moving towards positive y- axis with 1m/s
View Solution

