A planet revolves around the sun in elliptical orbit of eccentricity 'e'. If 'T' is the time period of the planet then the time spent by the planet between the ends of the minor axis and major axis close to the sun is
1. Tπ2e
2. T(2eπ−1)
2. Te2π
4. T(14−e2π)
The correct Answer is:D
To solve the problem of finding the time spent by a planet between the ends of the minor axis and the major axis close to the Sun in its elliptical orbit, we can follow these steps:
1. Understanding the Elliptical Orbit:
- An elliptical orbit has a major axis and a minor axis. The Sun is located at one of the foci of the ellipse.
2. Define Points:
- Let O be the center of the ellipse, P be the point on the major axis closest to the Sun, and L be the end of the minor axis.
3. Kepler's Second Law:
- According to Kepler's second law, the line segment joining a planet to the Sun sweeps out equal areas in equal times. This means that the area swept out by the planet in a given time is constant.
4. Calculate Total Area of the Ellipse:
- The area A of the ellipse is given by the formula:
A=πab
where a is the semi-major axis and b is the semi-minor axis.
5. Area Covered in One Revolution:
- The planet takes a time period T to cover the entire area A.
6. Area of Interest:
- We need to find the area between points P and L. This area can be determined by calculating the area of triangle SOL and subtracting it from the area OPL.
7. Area of Triangle SOL:
- The area of triangle SOL can be calculated using the formula:
AreaSOL=12×base×height=12×(ae)×b
where e is the eccentricity of the ellipse.
8. Area of Sector OPL:
- The area of sector OPL is one-fourth of the total area of the ellipse:
AreaOPL=14×πab
9. Calculate the Area Between P and L:
- The area between P and L is:
AreaPL=AreaOPL−AreaSOL
Substituting the values:
AreaPL=14πab−12aeb
10. Relate Area to Time:
- Since the area swept out is proportional to time, we can set up the relationship:
AreaPLT=AreaOPLT
11. Calculate Time t:
- The time t spent between points P and L can be expressed as:
t=T⋅AreaPLTotal Area=T⋅14πab−12aebπab
- Simplifying this gives:
t=T⋅(14−e2)
Final Result:
The time spent by the planet between the ends of the minor axis and major axis close to the Sun is:
t=T4−Te2
- An elliptical orbit has a major axis and a minor axis. The Sun is located at one of the foci of the ellipse.
- Let O be the center of the ellipse, P be the point on the major axis closest to the Sun, and L be the end of the minor axis.
- According to Kepler's second law, the line segment joining a planet to the Sun sweeps out equal areas in equal times. This means that the area swept out by the planet in a given time is constant.
- The area A of the ellipse is given by the formula:
A=πab
where a is the semi-major axis and b is the semi-minor axis.
- The planet takes a time period T to cover the entire area A.
- We need to find the area between points P and L. This area can be determined by calculating the area of triangle SOL and subtracting it from the area OPL.
- The area of triangle SOL can be calculated using the formula:
AreaSOL=12×base×height=12×(ae)×b
where e is the eccentricity of the ellipse.
- The area of sector OPL is one-fourth of the total area of the ellipse:
AreaOPL=14×πab
- The area between P and L is:
AreaPL=AreaOPL−AreaSOL
Substituting the values:
AreaPL=14πab−12aeb
- Since the area swept out is proportional to time, we can set up the relationship:
AreaPLT=AreaOPLT
- The time t spent between points P and L can be expressed as:
t=T⋅AreaPLTotal Area=T⋅14πab−12aebπab
- Simplifying this gives:
t=T⋅(14−e2)
The time spent by the planet between the ends of the minor axis and major axis close to the Sun is:
t=T4−Te2
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Universal law of Gravitations14videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - The Gravitational constant8videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason10videos
KINETIC THEORY
Similar Questions
A planet is revolving around the sun in an elliptical orbit having eccentricity e(=π4). If the time period of revolution is 16 months then find the time taken by the planet in going from A to B in months.
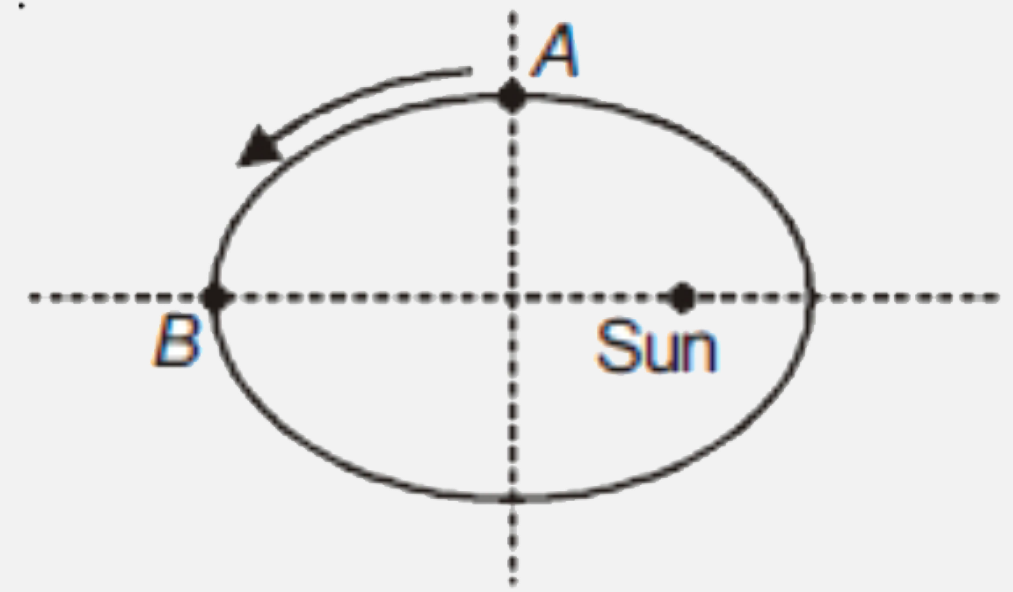 View Solution
View SolutionA planet revolves around the sun in an elliptical . The linear speed of the planet will be maximum at
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A planet revolves around the sun in an elliptical orbit. If vp and va are the velocities of the planet at the perigee and apogee respectively, then the eccentricity of the elliptical orbit is given by :
AvpvaBva−vpva+vpCvp+vavp−vaDvp−vavp+va - Question 2 - Select One
A planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at
 AABBCCDD
AABBCCDD - Question 3 - Select One
A planet revolves around the sun in an elliptical orbit. Suppose that the gravitational attraction between the sun and the planet suddenly disappear then the planet would move
Atowards the sun in a spiral pathBaway from the sun along a straight path with continuously increasing speedCwith constant speed along a tangential path to the oribtDtowards the sun along a straight path with constant speed
A planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
View SolutionA planet is revolving around the sun as shown in elliptical path. The correct option is
 View Solution
View SolutionA planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at
 View Solution
View SolutionA planet is moving round the sun in an elliptical orbit as shows. As the planet moves from A to B
 View Solution
View SolutionFor a planet revolving around Sun in an elliptical orbit, to obtain its velocity at any point we have to apply
View Solution

