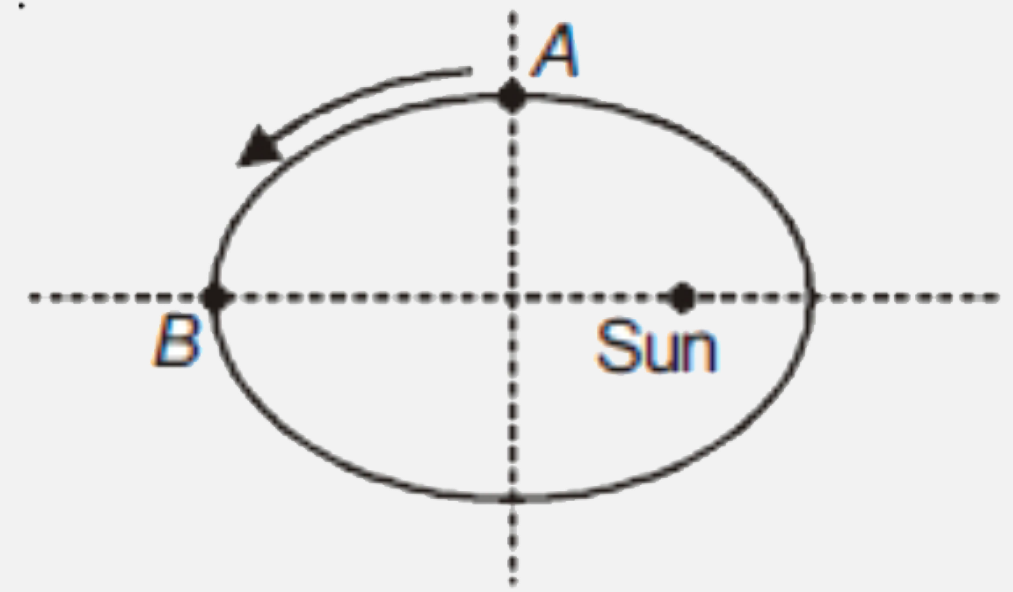
A planet is revolving around the sun as shown in elliptical path. The correct option is

its total energy is negative at D.
its angular momentum is constant
net torque on planet about sun is zero.
linear momentum of the planet is conserved.
The correct Answer is:A, B, C
For (A): for bounded system the total energy is always negative.
For (B): for centrel force field, angular momentum is always conserved
For (C): for central force field torque =0
for (D): in presence of external force, linear momentum is conserved.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 1 (Check your Grasp)28videos
GRAVITATION
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 2 (Brain Teasers)27videos
GRAVITATION
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)46videos
KINEMATICS-2D
Similar Questions
A planet is revolving around the sun in an elliptical orbit. Which out of the following remains constant.
(a) Linear speed (b) angular momentum
( c) kinetic energy (d) potential energy (e) total energy throughout its orbit.View SolutionA planet is revolving around the Sun in an elliptical orbit. Its closest distance from the Sun is r and farthest distance is R. If the orbital velocity of the planet closest to the Sun is v, then what is the velocity at the farthest point?
View SolutionA planet is revolving around the Sun in an elliptical orbit. Its closest distance from the sun is rmin. The farthest distance from the sun is rmax if the orbital angular velocity of the planet when it is nearest to the Sun ω then the orbital angular velocity at the point when it is at the farthest distance from the sun is
View SolutionA planet is revolving round the sun is elliptical orbit. Velocity at perigee position ( nearest) is v1 and at apogee position ( farthest) is v2. Both these velocities are perpendicular to the line joining centre of sun and planet. r1 is the minimum distance and r2 the maximum distance.
When the planet is at perigee position, it wants to revolve in a circular orbit by itselff. For this, value of GView SolutionA planet is revolving round the sun is elliptical orbit. Velocity at perigee position ( nearest) is v1 and at apogee position ( farthest) is v2. Both these velocities are perpendicular to the line joining centre of sun and planet. r1 is the minimum distance and r2 the maximum distance.
At apogee position suppose speed of planet is slightly decreased from v2, then what will happen to minimum distance r1 and maximum distance r2 in the subsequent motion.View SolutionA planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
View SolutionA planet is revolving around the sun in an elliptical orbit having eccentricity e(=π4). If the time period of revolution is 16 months then find the time taken by the planet in going from A to B in months.
 View Solution
View SolutionWhen a planet moves around the sun
View SolutionA planet is revolving round the sun in an elliptical orbit as shown in figure. Select correct alternative(s)
View SolutionA planet is revolving around the sun in an elliptcal orbit. Its KE is different for different points and the total energy is negative. Its linear momentum is not conserved the eccentricity decides the shape of the orbit.
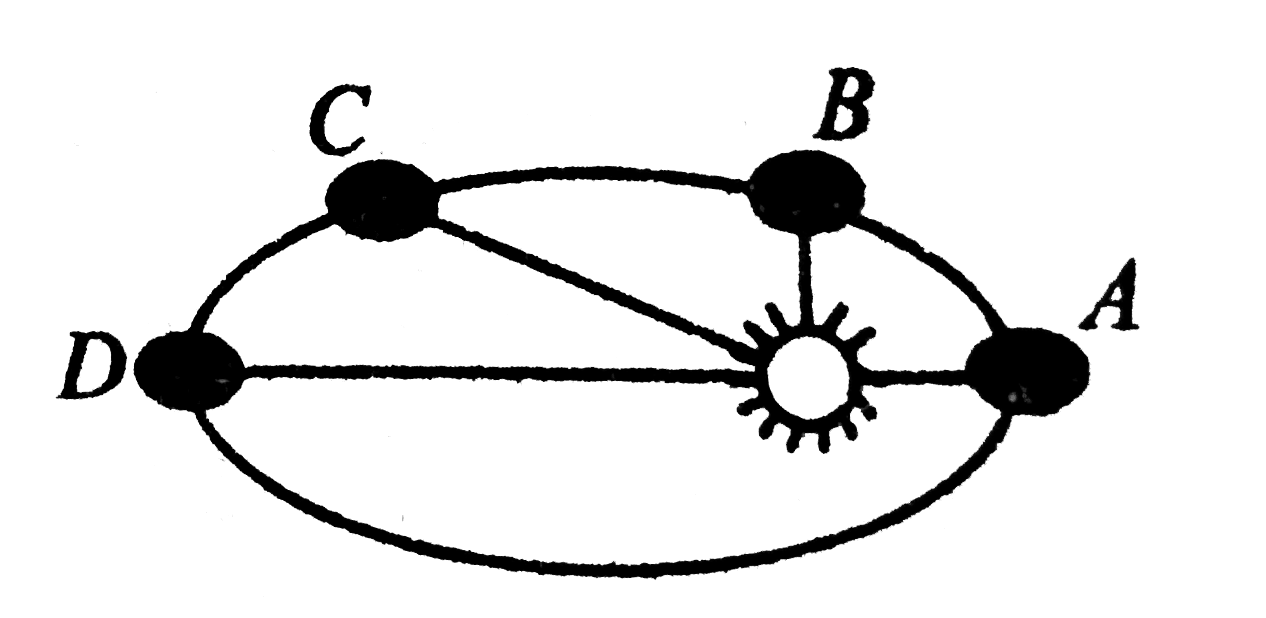
Net torque on the planet isView Solution

