A comet orbits the Sun in a highly elliptical orbit. Does the comet have a constant (a) linear speed (b) angular speed (c) angular momentum (d) kinetic energy (e) potential energy (f) total energy throughout its orbit? Neglect any mass loss of the comet when it comes very close to the Sun.
(i),(ii),(iii)
(iii),(iv),(v)
(iii) and (vi)
(ii),(iii) and (vi)
The correct Answer is:C
To determine whether the comet has constant values for linear speed, angular speed, angular momentum, kinetic energy, potential energy, and total energy throughout its elliptical orbit around the Sun, we can analyze each aspect step by step.
1. Linear Speed (a):
- In an elliptical orbit, the distance from the Sun (the focal point) changes as the comet moves along its path. According to Kepler's laws, the comet moves faster when it is closer to the Sun and slower when it is farther away.
- Conclusion: The linear speed of the comet is not constant.
2. Angular Speed (b):
- Angular speed is defined as the rate of change of angular displacement. Since the linear speed is not constant and the radius (distance from the Sun) changes, the angular speed also changes.
- Conclusion: The angular speed of the comet is not constant.
3. Angular Momentum (c):
- Angular momentum (L) is given by the formula L=mvr, where m is the mass, v is the linear speed, and r is the radius. In the absence of external torque, angular momentum is conserved.
- Since there are no external torques acting on the comet, its angular momentum remains constant throughout its orbit.
- Conclusion: The angular momentum of the comet is constant.
4. Kinetic Energy (d):
- Kinetic energy (KE) is given by the formula KE=12mv2. Since the linear speed is not constant, the kinetic energy will also vary as the speed changes.
- Conclusion: The kinetic energy of the comet is not constant.
5. Potential Energy (e):
- Gravitational potential energy (PE) is given by PE=−GMmr, where G is the gravitational constant, M is the mass of the Sun, m is the mass of the comet, and r is the distance from the Sun. As the comet moves closer or farther from the Sun, the potential energy changes.
- Conclusion: The potential energy of the comet is not constant.
6. Total Energy (f):
- The total mechanical energy (E) of the comet is the sum of its kinetic and potential energy: E=KE+PE. Although both kinetic and potential energy vary, the total energy remains constant throughout the orbit due to the conservation of mechanical energy in a closed system.
- Conclusion: The total energy of the comet is constant.
Summary of Results:
- (a) Linear speed: Not constant
- (b) Angular speed: Not constant
- (c) Angular momentum: Constant
- (d) Kinetic energy: Not constant
- (e) Potential energy: Not constant
- (f) Total energy: Constant
- In an elliptical orbit, the distance from the Sun (the focal point) changes as the comet moves along its path. According to Kepler's laws, the comet moves faster when it is closer to the Sun and slower when it is farther away.
- Conclusion: The linear speed of the comet is not constant.
- Angular speed is defined as the rate of change of angular displacement. Since the linear speed is not constant and the radius (distance from the Sun) changes, the angular speed also changes.
- Conclusion: The angular speed of the comet is not constant.
- Angular momentum (L) is given by the formula L=mvr, where m is the mass, v is the linear speed, and r is the radius. In the absence of external torque, angular momentum is conserved.
- Since there are no external torques acting on the comet, its angular momentum remains constant throughout its orbit.
- Conclusion: The angular momentum of the comet is constant.
- Kinetic energy (KE) is given by the formula KE=12mv2. Since the linear speed is not constant, the kinetic energy will also vary as the speed changes.
- Conclusion: The kinetic energy of the comet is not constant.
- Gravitational potential energy (PE) is given by PE=−GMmr, where G is the gravitational constant, M is the mass of the Sun, m is the mass of the comet, and r is the distance from the Sun. As the comet moves closer or farther from the Sun, the potential energy changes.
- Conclusion: The potential energy of the comet is not constant.
- The total mechanical energy (E) of the comet is the sum of its kinetic and potential energy: E=KE+PE. Although both kinetic and potential energy vary, the total energy remains constant throughout the orbit due to the conservation of mechanical energy in a closed system.
- Conclusion: The total energy of the comet is constant.
- (a) Linear speed: Not constant
- (b) Angular speed: Not constant
- (c) Angular momentum: Constant
- (d) Kinetic energy: Not constant
- (e) Potential energy: Not constant
- (f) Total energy: Constant
Topper's Solved these Questions
- GRAVITATIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Geostationary and Polar satellites
7 Videos
- GRAVITATIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Weightlessness
2 Videos
- GRAVITATIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Earth Satellite
4 Videos
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
Similar Questions
A planet is revolving around the sun in an elliptical orbit. Which out of the following remains constant.
(a) Linear speed (b) angular momentum
( c) kinetic energy (d) potential energy (e) total energy throughout its orbit.
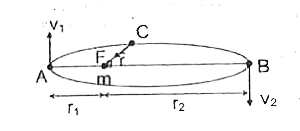
View SolutionIn the figure shown a planet moves in an elliptical orbit around the sun. Compare the speeds, linear and angular momenta at the points A and B.
View SolutionA star like the sun has serveral bodies moving around it at different distance. Consider that all of them are moving in circular orbits. Let r be the distance of the body from the centre of the star and let its linear velocity be υ, angular velocity ω, kinetic energy K, gravitational potential energy U, total energy E and angular momentum L. As the radius r of the orbit increase, determine which of the above quantities increase and which ones decrease.
View SolutionA planet is moving in an elliptic orbit. If T,V,E and L stand, respectively, for its kinetic energy, gravitational potential energy, total energy and angular momentum about the centre of force, then
View SolutionA comet revolves around the sun in an eliptical orbit. When it is closest to the sun at a distance d, its corresponding kinetic energy is k0. If it is farthest from the sun at distance 3d then the corresponding kinetic energy will be
View SolutionA rod of mass m spins with an angular speed ω=√gl, Find its a. kinetic energy of rotation. b. kinetic energy of translation c. total kinetic energy.

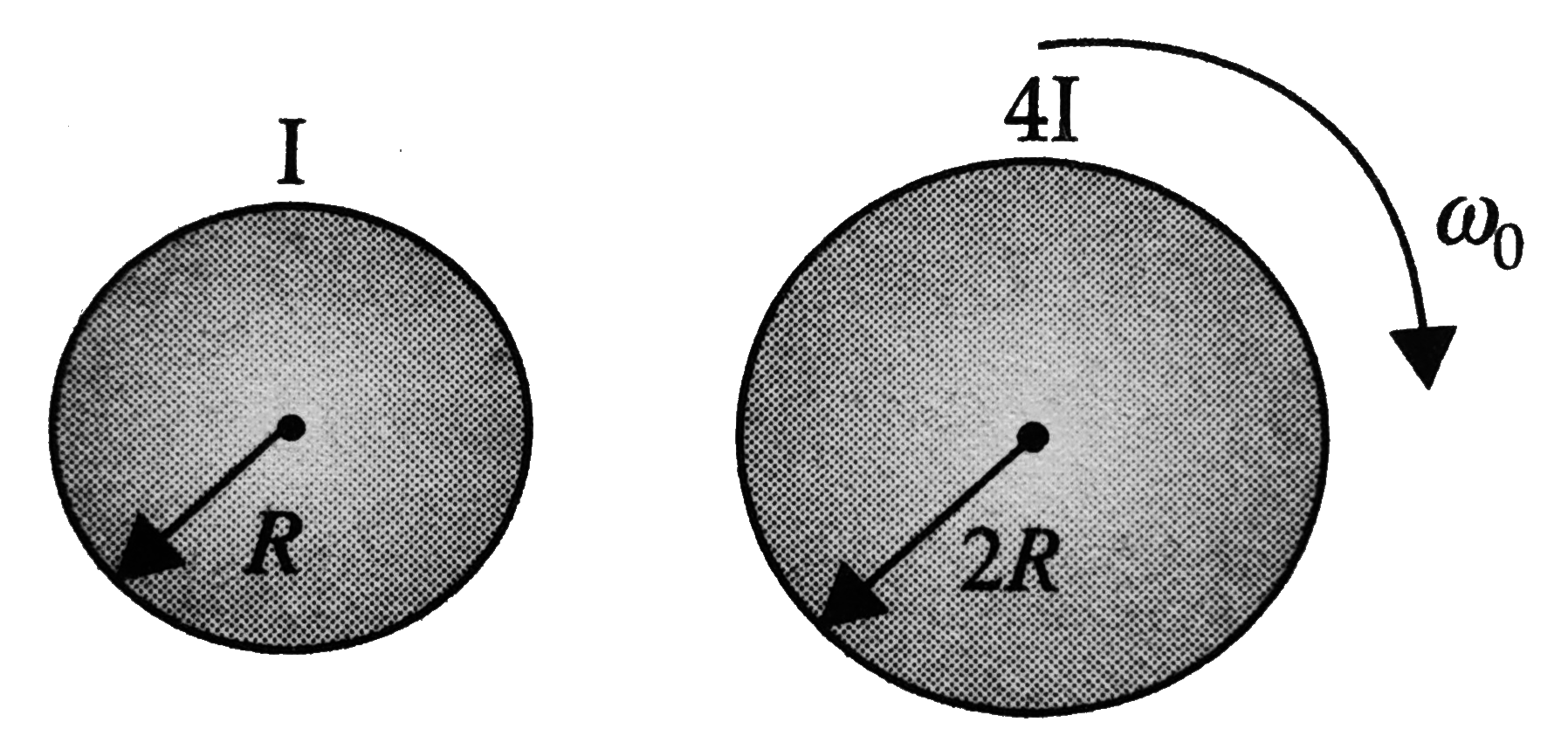
View SolutionTwo cylinders having radii 2R and R and moment of inertia 4I and I about their central axes are supported by axles perpendicular to their planes. The large cylinder is initially rotating clockwise with angular velocity ω0. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually slipping ceases and the two cylinders rotate at constant rates in opposite directions. During this
(A) angular momentum of system is conserved
(B) kinetic energy is conserved
(C neither the angular momentum nor the kinetic energy is conserved
(D) both the angular momentum and kinetic energy are conserved
View SolutionA planet is revolving around the sun in an elliptcal orbit. Its KE is different for different points and the total energy is negative. Its linear momentum is not conserved the eccentricity decides the shape of the orbit.
Linear momentum of the planet is
View SolutionA planet is revolving around the sun in an elliptcal orbit. Its KE is different for different points and the total energy is negative. Its linear momentum is not conserved the eccentricity decides the shape of the orbit.
Net torque on the planet is
View SolutionA planet is revolving around the sun in an elliptcal orbit. Its KE is different for different points and the total energy is negative. Its linear momentum is not conserved the eccentricity decides the shape of the orbit.
Velocity of the planet is minimum at
View Solution
