Two stars each of mass M and radius R are approaching each other for a head-on collision. They start approaching each other when their separation is r>>R. If their speed at this separation are negligible, the speed v with which they collide would be
1. v=√GM(1R−1r)
2. v=√GM(12R−1r)
3. v=√GM(1R+1r)
4. v=√GM(12R+1r)
The correct Answer is:B
To solve the problem of finding the speed v with which two stars collide, we can use the principle of conservation of energy. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Initial Conditions
The two stars, each of mass M and radius R, start approaching each other from a separation r where r≫R. At this point, their speeds are negligible, meaning their initial kinetic energy is zero.
Hint: Remember that when speeds are negligible, kinetic energy is zero.
Step 2: Calculate Initial Potential Energy
The gravitational potential energy U between two masses M separated by a distance r is given by:
Ui=−GM2r
where G is the gravitational constant.
Hint: Use the formula for gravitational potential energy to find the initial energy.
Step 3: Calculate Final Energy at Collision
When the stars collide, their centers are separated by a distance equal to 2R (since each star has a radius R). At this point, they have kinetic energy due to their motion. The final potential energy Uf when they are at the point of collision is:
Uf=−GM22R
The total kinetic energy K of the two stars when they collide is:
K=12Mv2+12Mv2=Mv2
Hint: Remember to account for both stars when calculating the total kinetic energy.
Step 4: Apply Conservation of Energy
By the conservation of energy, the initial potential energy must equal the sum of the final potential energy and the kinetic energy:
Ui+0=Uf+K
Substituting the expressions we found:
−GM2r=−GM22R+Mv2
Hint: Set up the equation based on conservation of energy to relate initial and final energies.
Step 5: Rearranging the Equation
Rearranging the equation gives:
Mv2=−GM2r+GM22R
Factoring out GM2:
Mv2=GM2(12R−1r)
Dividing both sides by M:
v2=GM(12R−1r)
Hint: Isolate v2 to find the expression in terms of G, M, R, and r.
Step 6: Solve for v
Taking the square root of both sides gives:
v=√GM(12R−1r)
Hint: Remember to take the square root to find the speed v.
Final Answer
Thus, the speed v with which the stars collide is:
v=√GM(12R−1r)
The two stars, each of mass M and radius R, start approaching each other from a separation r where r≫R. At this point, their speeds are negligible, meaning their initial kinetic energy is zero.
The gravitational potential energy U between two masses M separated by a distance r is given by:
Ui=−GM2r
where G is the gravitational constant.
When the stars collide, their centers are separated by a distance equal to 2R (since each star has a radius R). At this point, they have kinetic energy due to their motion. The final potential energy Uf when they are at the point of collision is:
Uf=−GM22R
The total kinetic energy K of the two stars when they collide is:
K=12Mv2+12Mv2=Mv2
By the conservation of energy, the initial potential energy must equal the sum of the final potential energy and the kinetic energy:
Ui+0=Uf+K
Substituting the expressions we found:
−GM2r=−GM22R+Mv2
Rearranging the equation gives:
Mv2=−GM2r+GM22R
Factoring out GM2:
Mv2=GM2(12R−1r)
Dividing both sides by M:
v2=GM(12R−1r)
Taking the square root of both sides gives:
v=√GM(12R−1r)
Thus, the speed v with which the stars collide is:
v=√GM(12R−1r)
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Geostationary and Polar satellites7videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Weightlessness2videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Earth Satellite4videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason10videos
KINETIC THEORY
Similar Questions
Two stars each of 1 solar mass (=2×1030kg) are approaching each other for a head-on collision. When they are at a distance 109km apart their speeds are negligible . What is the speed with which they collide? The radius of each star is 104km. Assume the starts to remain undistorted untile they collide, G=6.67×10−11Nm2kg−2.
View SolutionTwo starts each of one solar mass (=2×1030kg) are approaching each other for a head on collision. When they are a distance 109km. their speeds are negligible. What is the speed with which they collide? The radius of each star is 104km. Assume the stars to remain undistorted until they collide. (Use the known value of G).
View SolutionWhat type of forces come into action when two atoms approach each other?
View SolutionDuring the formation of a bond when atoms approach each other the potential energy decreases.(T/F)
View SolutionTwo particles of mass m1 and m2 are approaching towards each other under their mutual gravitational field. If the speed of the particle is v, the speed of the center of mass of the system is equal to :
View SolutionThree solid spheres each of mass m and radius R are released from the position shown in Fig. What is the speed of any one sphere at the time of collision?
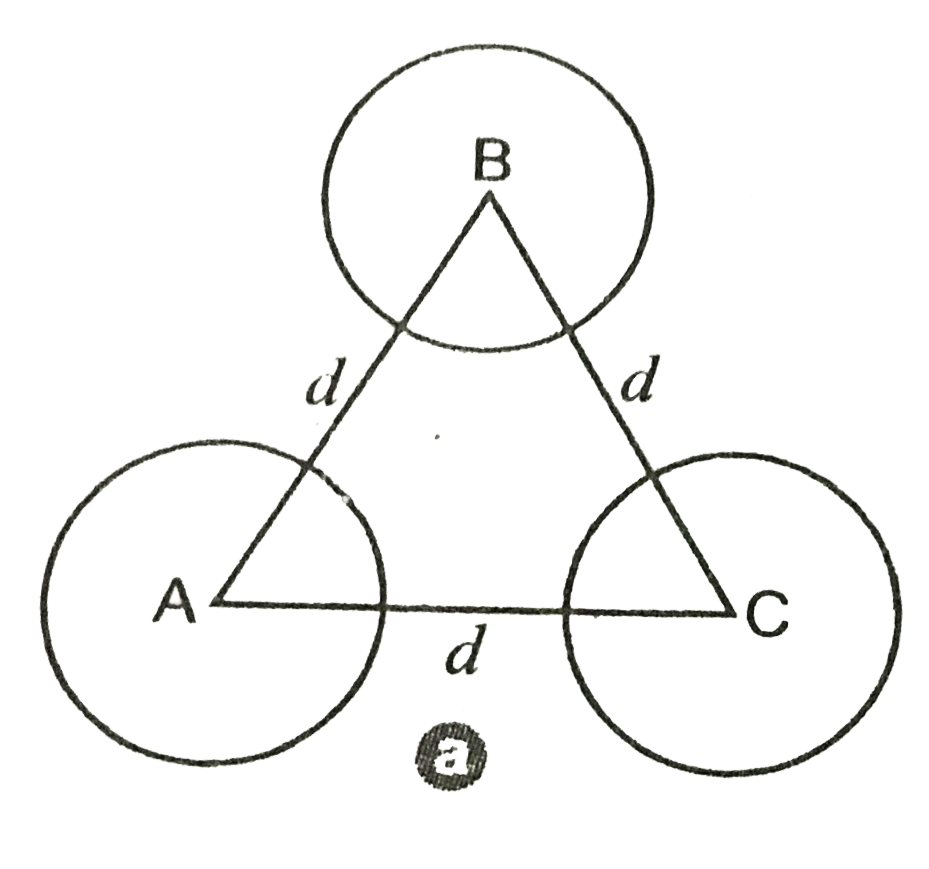 View Solution
View SolutionThree rings each of mass m and radius r are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is
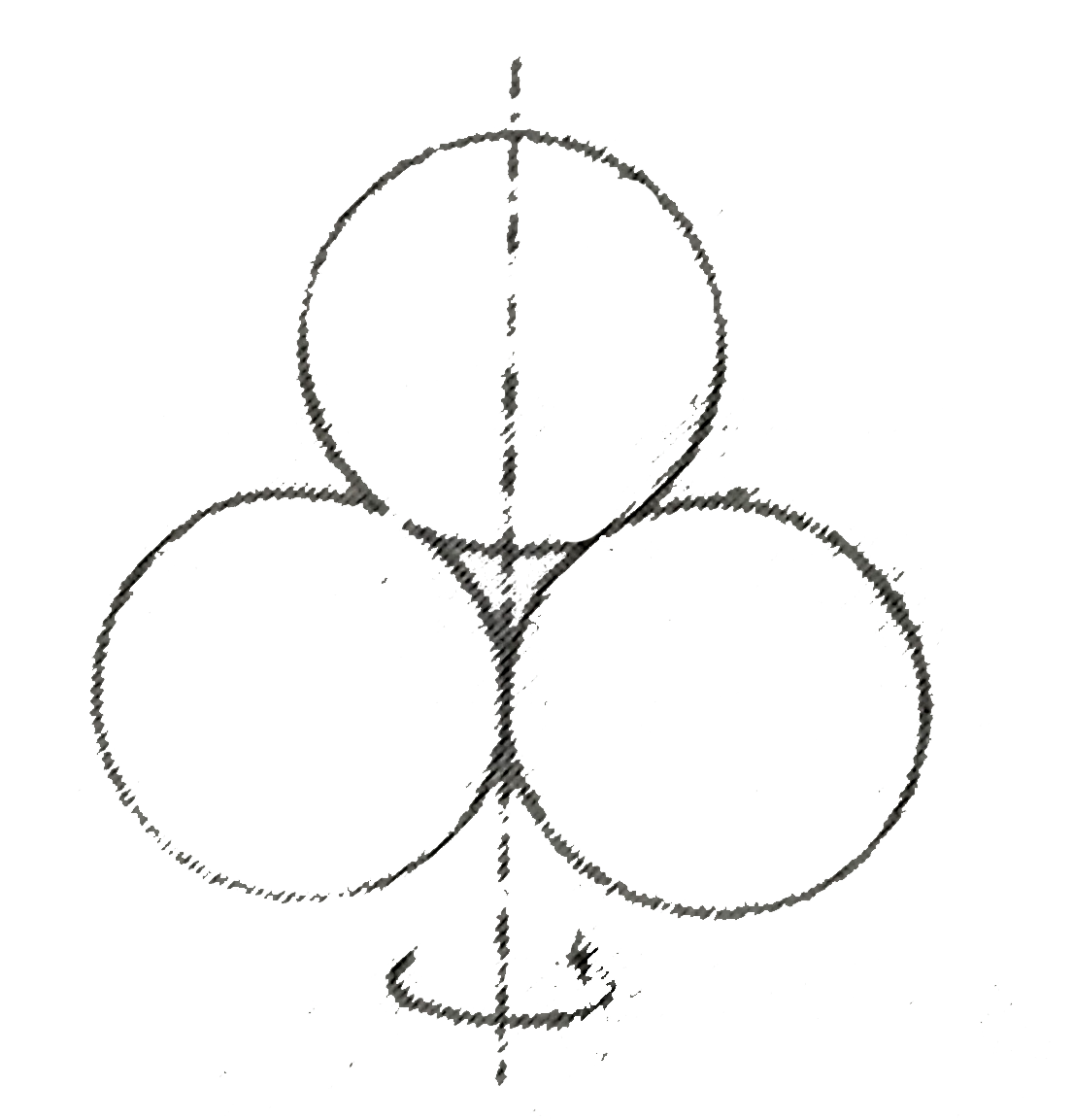 View Solution
View SolutionTwo spherical bodies of masses 2M and M and radii 3R and R respectively are held at a distance 16R from each other in free space. When they are released they start approaching each other due to the gravitational force of attraction , then find
(a) the ratio of their accelerations during their motion
(b) their velocitites at the time of impact.
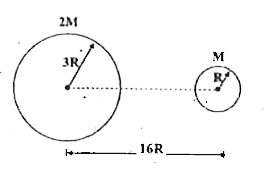 View Solution
View SolutionFour particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:
View SolutionFour particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is:
View Solution

