Question

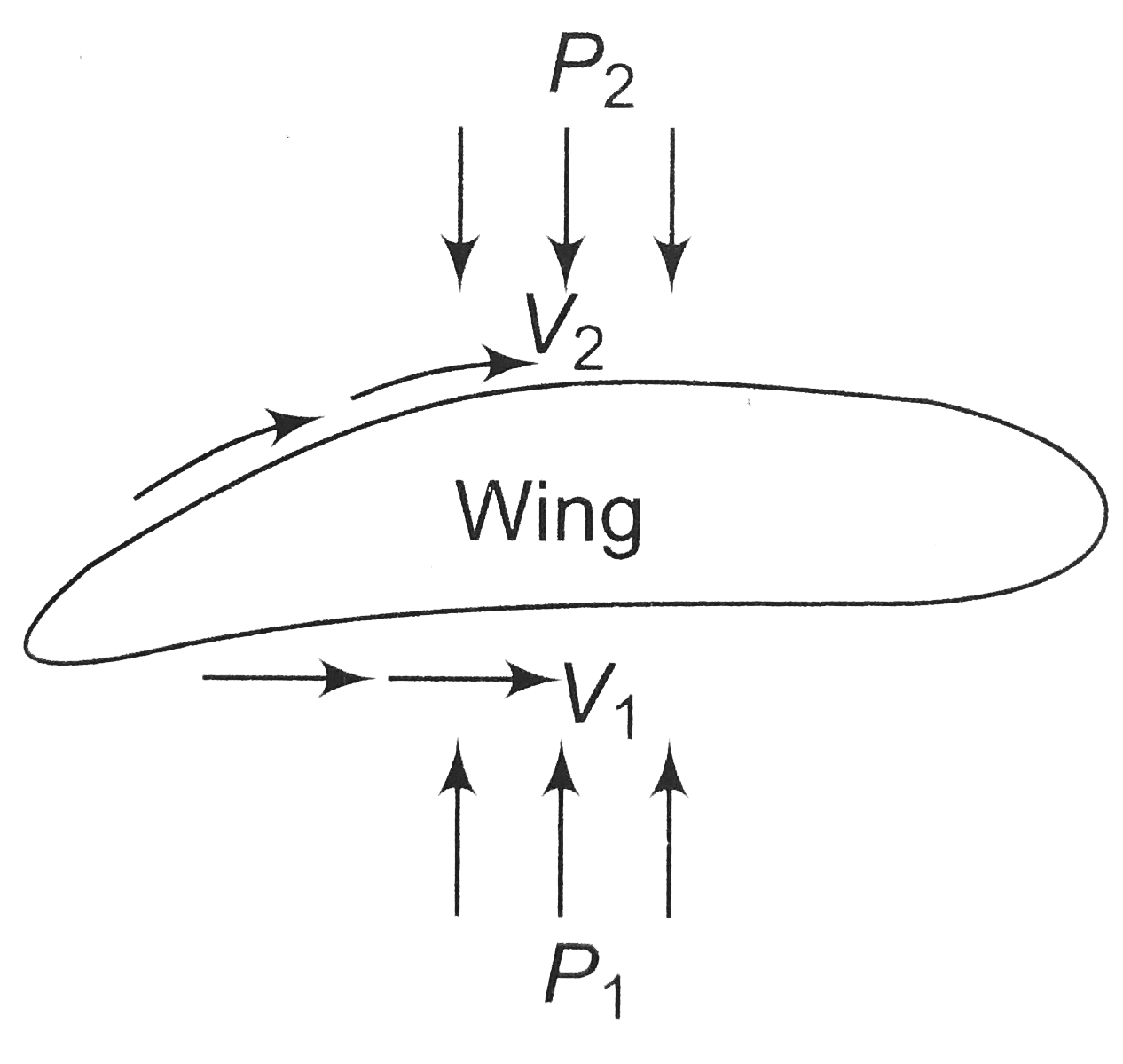
A plane is in level flight at constant speed and each of its two wings has an area of $25m^2$ . If the speed of the air on the upper and lower surfaces of the wing are $270km{h}^{-1}$ and '234 km h^(-1)' respectively, then the mass of the plane is (Take the density of the air $=1kg{m}^{-3}$)

Options

A. 1550 kg
B. 1750 kg
C. 3500 kg
D. 3200 kg

Answer

C

Explanation

To solve the problem step by step, we will follow these calculations:

Step 1: Convert the speeds from km/h to m/s
We are given the speeds of the air on the upper and lower surfaces of the wing:
- Speed on the upper surface (V2) = 270 km/h
- Speed on the lower surface (V1) = 234 km/h

To convert these speeds to meters per second (m/s), we use the conversion factor \( \frac{5}{18} \):
\( V1 = 234 \times \frac{5}{18} = 65 \, \text{m/s} \)
\( V2 = 270 \times \frac{5}{18} = 75 \, \text{m/s} \)

Step 2: Calculate the pressure difference using Bernoulli's principle
According to Bernoulli's principle, the pressure difference between the upper and lower surfaces of the wing can be expressed as:
\( P1 - P2 = \frac{1}{2} \rho (V2^2 - V1^2) \)
Where:
- \( \rho \) = density of air = 1 kg/m³

Substituting the values:
\( P1 - P2 = \frac{1}{2} \times 1 \times (75^2 - 65^2) \)

Calculating \( 75^2 \) and \( 65^2 \):
\( 75^2 = 5625, \quad 65^2 = 4225 \)
Thus,
\( P1 - P2 = \frac{1}{2} \times 1 \times (5625 - 4225) = \frac{1}{2} \times 1 \times 1200 = 600 \, \text{N/m}^2 \)

Step 3: Calculate the total upward force on the wings
The total upward force (F) acting on the wings can be calculated using the pressure difference and the area of the wings:
\( F = (P1 - P2) \times A \)
Where:
- \( A \) = total area of the wings = \( 25 \, \text{m}^2 \times 2 = 50 \, \text{m}^2 \)

Substituting the values:
\( F = 600 \, \text{N/m}^2 \times 50 \, \text{m}^2 = 30000 \, \text{N} \)

Step 4: Relate the upward force to the weight of the plane
In level flight, the upward force equals the weight of the plane (mg):
\( mg = 30000 \, \text{N} \)

Step 5: Calculate the mass of the plane
To find the mass (m) of the plane, we use the acceleration due to gravity (g = 10 m/s²):
\( m = \frac{F}{g} = \frac{30000 \, \text{N}}{10 \, \text{m/s}^2} = 3000 \, \text{kg} \)

Final Answer
The mass of the plane is \( 3000 \, \text{kg} \).

---