Question

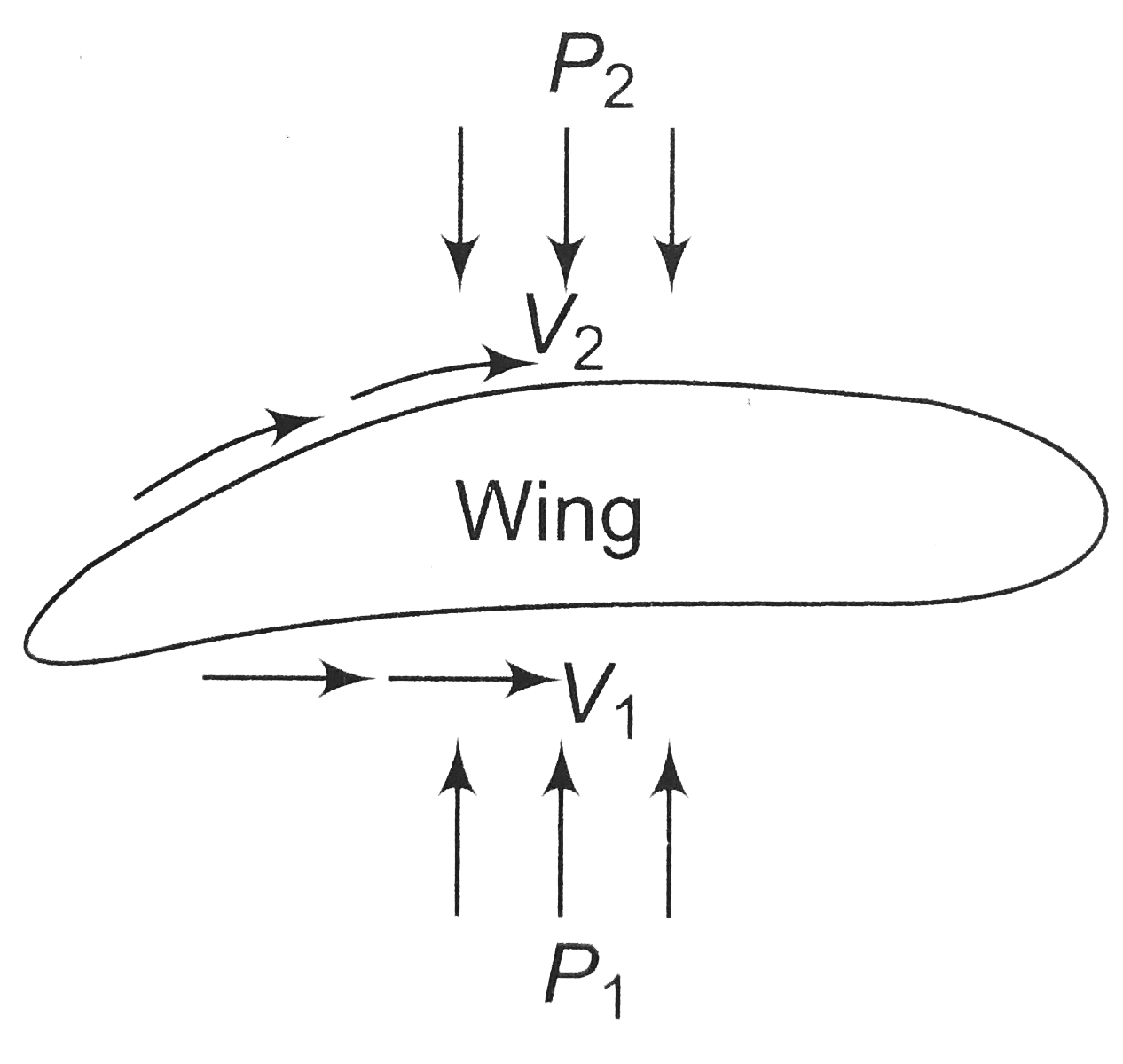
A plane is in level flight at constant speed and each of its wings has an area of $25m^2$. If the speed of the air is $180km/h$ over the upper wing surface, determine the plane's mass . (Take air density to be $1kg/m^3$). $g=9.8m/s^2$.

Explanation

To determine the mass of the plane in level flight, we can follow these steps:

1. Convert Speeds from km/h to m/s:
- The speed of air over the lower wing (V1) is given as 180 km/h.
- Convert V1 to m/s:
\( V1 = 180 \times \frac{1000}{3600} = 50 \text{ m/s} \)
- The speed of air over the upper wing (V2) is given as 234 km/h.
- Convert V2 to m/s:
\( V2 = 234 \times \frac{1000}{3600} = 65 \text{ m/s} \)

2. Calculate the Pressure Difference:
- Use Bernoulli's equation to find the pressure difference (P1 - P2) between the lower and upper wings:
\( P1 - P2 = \frac{1}{2} \rho (V2^2 - V1^2) \)
- Given that air density (\(\rho\)) is 1 kg/m³, substitute the values:
\( P1 - P2 = \frac{1}{2} \times 1 \times (65^2 - 50^2) \)
- Calculate \(65^2\) and \(50^2\):
\( 65^2 = 4225, \quad 50^2 = 2500 \)
- Thus, the pressure difference becomes:
\( P1 - P2 = \frac{1}{2} \times 1 \times (4225 - 2500) = \frac{1}{2} \times 1 \times 1725 = 862.5 \text{ Pa} \)

3. Calculate the Total Lift Force:
- The total lift force (F) acting on the wings can be calculated using the area (A) of the wings:
\( F = (P1 - P2) \times A \)
- The area of each wing is given as 25 m², so for both wings:
\( A = 2 \times 25 = 50 \text{ m}^2 \)
- Therefore, the lift force is:
\( F = 862.5 \times 50 = 43125 \text{ N} \)

4. Relate Lift Force to Weight:
- In level flight, the lift force equals the weight of the plane:
\( F = m \cdot g \)
- Where \(g = 9.8 \text{ m/s}^2\). Thus, we can find the mass (m) of the plane:
\( m = \frac{F}{g} = \frac{43125}{9.8} \approx 4400.51 \text{ kg} \)

5. Final Result:
- Rounding to the nearest whole number, the mass of the plane is approximately:
\( m \approx 4400 \text{ kg} \)