Two cylinder having m1g and m2g of a gas at pressure P1 and P2 respectively are put in cummunication with each other, temperature remaining constant. The common pressure reached will be
P1P2(m1+m2)P2m1+P1m2
P1P2m1P2m1+P1m2
m1m2(P1+P2)P2m1(P1+P2)
m1m2P2P2m1+P1m2
The correct Answer is:A
To find the common pressure reached when two cylinders containing gases at different pressures are put in communication with each other, we can follow these steps:
1. Understand the Problem: We have two cylinders with masses of gas m1g and m2g at pressures P1 and P2 respectively. When they are connected, they will reach a common pressure P while maintaining a constant temperature.
2. Use the Ideal Gas Law: The ideal gas equation is given by:
PV=nRT
This can also be expressed in terms of mass:
PV=mMRT
where m is the mass of the gas, M is the molar mass, R is the universal gas constant, and T is the temperature.
3. Write the Equations for Each Cylinder:
- For the first cylinder:
P1V1=m1MRT(Equation 1)
- For the second cylinder:
P2V2=m2MRT(Equation 2)
4. Combine the Two Cylinders: When the two cylinders are put in communication, they will have a total volume V1+V2 and a total mass m1+m2. The common pressure P can be expressed as:
P(V1+V2)=m1+m2MRT(Equation 3)
5. Substitute Equations 1 and 2 into Equation 3:
- From Equation 1, we can express V1 as:
V1=m1RTP1M
- From Equation 2, we can express V2 as:
V2=m2RTP2M
6. Substituting into Equation 3:
P(m1RTP1M+m2RTP2M)=m1+m2MRT
7. Simplify the Equation: Cancel RT and M from both sides:
P(m1P1+m2P2)=m1+m2
8. Rearranging for Common Pressure P:
P=(m1+m2)(m1P1+m2P2)
9. Final Expression: To express this in a more usable form, we can multiply the numerator and denominator by P1P2:
P=(m1+m2)P1P2m1P2+m2P1
Final Answer:
The common pressure reached when the two cylinders are put in communication is:
P=(m1+m2)P1P2m1P2+m2P1
PV=nRT
This can also be expressed in terms of mass:
PV=mMRT
where m is the mass of the gas, M is the molar mass, R is the universal gas constant, and T is the temperature.
- For the first cylinder:
P1V1=m1MRT(Equation 1)
- For the second cylinder:
P2V2=m2MRT(Equation 2)
P(V1+V2)=m1+m2MRT(Equation 3)
- From Equation 1, we can express V1 as:
V1=m1RTP1M
- From Equation 2, we can express V2 as:
V2=m2RTP2M
P(m1RTP1M+m2RTP2M)=m1+m2MRT
P(m1P1+m2P2)=m1+m2
P=(m1+m2)(m1P1+m2P2)
P=(m1+m2)P1P2m1P2+m2P1
The common pressure reached when the two cylinders are put in communication is:
P=(m1+m2)P1P2m1P2+m2P1
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXEMPLAR PROBLEMS8videos
KINETIC THEORY
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - ASSERTION & REASON10videos
KINETIC THEORY
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - SPECIFIC CEAT CAPACITY13videos
KINETIC THEORY
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion And Reason15videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason15videos
LAWS OF MOTION
Similar Questions
Three containes of the same volume contain three different gases. The masses of the molecules are m1,m2 and m3 and the number of molecules in their respective containers are N1,N2 and N3. The gas pressure in the containers are P1,P2 and P3 respectively. All the gases are now mixed and put in one of the containers. The pressure P of mixture will be
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionGaseous system is placed with pressure P1, volume V1 and temperature T1, it has undergone thermodynamic changes where temperature is remaining constant, it is
View SolutionV vs T curves at constant pressure P1 and P2 for an ideal gas are shown below
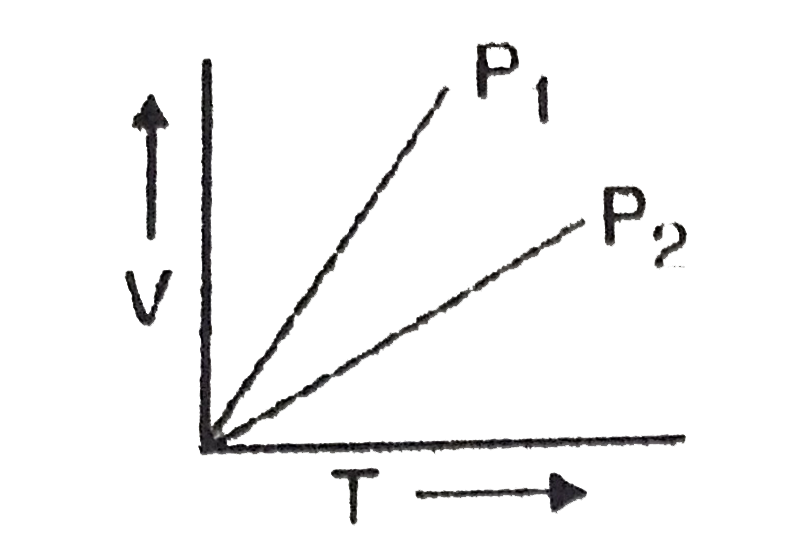
Which is correct ?View SolutionTwo vessels of volume (V1)and(V2) contain the same ideal gas. The pressures in the vessels are (P1)and(P2) and the temperatures are (T1)and(T2) respectively . The two vessels are now connected to each other through a narrow tube. Assuming that no heat is exchanged between the surrounding and the vessels, find the common pressure and temperature attained after the connection.
View SolutionTwo adiabatic containers have volumes V1 and V2 respectively. The first container has monoatomic gas at pressure p1 and temperature T1. The second container has another monoatomic gas at pressure p2 and temperature T2. When the two containers are connected by a narrow tube, the final temperature and pressure of the gases in the containers are P and T respectively. Then
View SolutionTwo idential container joined by a small pipe initially contain the same gas at pressure p0 and absolute temperature T0. One container is now maintained at the same temperature while the other is heated to 2T0. The common pressure of the gas
View SolutionTwo solutions of KNO3 and CH3COOH are prepared separately. The molarity of both is 0.1M and osmotic pressure is P1 and P2, respectively.
The correct relationship between the osmotic pressure isView SolutionFor an ideal gas V−T curves at constant pressure P1 & P2 are shown in figure, from the figure
_E01_061_Q01.png) View Solution
View Solution

