Sounds waves travel at 350m/s through a warm air and at 3500m/s through brass. The wavelength of a 700Hz. Acoustic wave as it enters brass from warm air
decreases by a factor 10
increases by a factor 10
increases by a factor 10
decreases by a factor 20
The correct Answer is:C
To find the wavelength of a 700 Hz acoustic wave as it enters brass from warm air, we can follow these steps:
Step 1: Understand the relationship between speed, frequency, and wavelength
The fundamental relationship for waves is given by the equation:
V=f⋅λ
where:
- V is the speed of the wave,
- f is the frequency,
- λ is the wavelength.
Step 2: Identify the given values
From the question, we have:
- Speed of sound in warm air, V1=350m/s
- Speed of sound in brass, V2=3500m/s
- Frequency of the wave, f=700Hz
Step 3: Calculate the wavelength in warm air
Using the wave equation for warm air:
V1=f⋅λ1
Substituting the known values:
350=700⋅λ1
To find λ1:
λ1=350700=0.5m
Step 4: Calculate the wavelength in brass
Now, using the wave equation for brass:
V2=f⋅λ2
Substituting the known values:
3500=700⋅λ2
To find λ2:
λ2=3500700=5m
Step 5: Determine the change in wavelength
Now we compare λ2 with λ1:
- λ1=0.5m
- λ2=5m
To find the factor by which the wavelength increases:
Factor=λ2λ1=50.5=10
Conclusion
The wavelength of the 700 Hz acoustic wave increases by a factor of 10 as it enters brass from warm air.
The fundamental relationship for waves is given by the equation:
V=f⋅λ
where:
- V is the speed of the wave,
- f is the frequency,
- λ is the wavelength.
From the question, we have:
- Speed of sound in warm air, V1=350m/s
- Speed of sound in brass, V2=3500m/s
- Frequency of the wave, f=700Hz
Using the wave equation for warm air:
V1=f⋅λ1
Substituting the known values:
350=700⋅λ1
To find λ1:
λ1=350700=0.5m
Now, using the wave equation for brass:
V2=f⋅λ2
Substituting the known values:
3500=700⋅λ2
To find λ2:
λ2=3500700=5m
Now we compare λ2 with λ1:
- λ1=0.5m
- λ2=5m
Factor=λ2λ1=50.5=10
The wavelength of the 700 Hz acoustic wave increases by a factor of 10 as it enters brass from warm air.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - HOTS8videos
WAVES
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - EXEMPLER10videos
WAVES
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason15videos
UNITS AND MEASUREMENTS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - Assertion And Reason15videos
WORK , ENERGY AND POWER
Similar Questions
When a sound wave travels from water to air , it
View SolutionA wave travelling along the length of a string is shown in Fig. 14.4.12. Using the scale on the given axis, find
(i) The amplitude of the wave
(ii) The wavelength of the wave
(iii) If the frequency of the wave is 10 Hz, What is the speed of the wave?
(iv) What is the initial phase of the wave ?
(v) What is the phase difference between two points separated by a distance 10 cm ?
(vi) If this wave is made to travel through water what is the wavelength of the wave, if the speed of, the waves in water is 10 m/s.
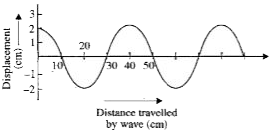 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Sound waves travel at 350 m/s through warm air and at 3,500m/s through brass. What happens to the wavelength of a 700 Hz acoustic wave as it enters brass from warm air?
AIt decreases by a factor of 20BIt decreases by a factor of 10CIt increase by a factor of 10DIt increase by a factor of 20 - Question 2 - Select One
A light wave, travelling at 3×108m/s has a frequency of 6×1015 Hz. What is its wavelength?
A5×10−8mB2×10−7mC5×10−7mD5×10−6m - Question 3 - Select One
A sound wave travels with a velocity of 300 m s−1 through a gas. 9 beats are produced in 3 s when two waves pass through it simultaneously. lf one of the waves has 2 m wavelength, the wavelength of the other wave is a) 1.98 m b) 2.04 m c) 2.06 m d) 1.99 m
A1.98 mB2.04 mC2.06 mD1.99 m
The frequency of a car horm is 400 Hz. If the horn is honked as the car moves with a speed uS=34ms through still air towards a stationary receiver, the wavelength of the sound passing the receiver is [velocity of sound is 340ms]
View SolutionA submarin Travels through water at a speed of 8.00ms, emitting a sonar wave at a frequency of 1400 Hz. The speed of sound in the water is 1533 m/s. What frequency is detected by an observer riding on submarine of velocity 9.00msas the submarines approach each other?
View SolutionSix antinodes are observed in the air column when a standing wave forms in a Kundt's tube . What is the length of the air column if steel bar of 1m length is clamped at the middle .
The velocity of sound in steel is 5250m/s and in air 343m/s.View SolutionTwo sound waves of wavelength 1m and 1.01m in a gas produce 10 beats in 3s. The velocity of sound in the gas is
View SolutionWhen sound waves travel from air to water which of these remains constant ?
View Solution

