When a string fixed at its both ends vibrates in 1 loop, 2 loops, 3 loops and 4 loops, the frequencies are in the ratio
1 : 1 : 1 : 1
1 : 2 : 3 : 4
4 : 3 : 2 : 1
1 : 4 : 9 : 16
The correct Answer is:B
To find the ratio of frequencies when a string fixed at both ends vibrates in different modes (1 loop, 2 loops, 3 loops, and 4 loops), we can follow these steps:
Step 1: Understand the relationship between loops and wavelength
When a string vibrates in n loops, the length of the string (L) is related to the wavelength (λ) by the formula:
n⋅λ2=L
This means that the wavelength can be expressed as:
λ=2Ln
Step 2: Relate frequency to wavelength
The frequency (f) of a wave is related to its speed (v) and wavelength (λ) by the formula:
f=vλ
Substituting the expression for wavelength from Step 1, we get:
f=v2Ln=vn2L
Step 3: Calculate frequencies for different modes
Now we can calculate the frequencies for n = 1, 2, 3, and 4:
- For n = 1 (1 loop):
f1=v⋅12L=v2L
- For n = 2 (2 loops):
f2=v⋅22L=2v2L=vL
- For n = 3 (3 loops):
f3=v⋅32L=3v2L
- For n = 4 (4 loops):
f4=v⋅42L=4v2L=2vL
Step 4: Write the frequencies in ratio form
Now we can express the frequencies in ratio form:
- f1:f2:f3:f4=v2L:vL:3v2L:2vL
Step 5: Simplify the ratio
To simplify the ratio, we can eliminate v and L:
- f1:f2:f3:f4=1:2:3:4
Final Answer
Thus, the frequencies are in the ratio:
1:2:3:4
When a string vibrates in n loops, the length of the string (L) is related to the wavelength (λ) by the formula:
n⋅λ2=L
This means that the wavelength can be expressed as:
λ=2Ln
The frequency (f) of a wave is related to its speed (v) and wavelength (λ) by the formula:
f=vλ
Substituting the expression for wavelength from Step 1, we get:
f=v2Ln=vn2L
Now we can calculate the frequencies for n = 1, 2, 3, and 4:
- For n = 1 (1 loop):
f1=v⋅12L=v2L
- For n = 2 (2 loops):
f2=v⋅22L=2v2L=vL
- For n = 3 (3 loops):
f3=v⋅32L=3v2L
- For n = 4 (4 loops):
f4=v⋅42L=4v2L=2vL
Now we can express the frequencies in ratio form:
- f1:f2:f3:f4=v2L:vL:3v2L:2vL
To simplify the ratio, we can eliminate v and L:
- f1:f2:f3:f4=1:2:3:4
Thus, the frequencies are in the ratio:
1:2:3:4
Topper's Solved these Questions
- WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - HOTS
8 Videos
- WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - EXEMPLER
10 Videos
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason
15 Videos
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
A string fixed at its both ends vibrates in 5 loops as shown in the figure. The total number of nodes and antinodes are respectively
 A5,6B6,5C7,4D4,7
A5,6B6,5C7,4D4,7
(A): When a stretched string vibrates in two segments, then all the vibrating particles in first half of the string are in out of phase to that of in the remaining of the string
(R): In a stationary wave the phase difference between the vibrating particles in two consecutive loops is trad.
View SolutionA 660 Hz tuning fork sets up vibration in a string clamped at both ends. The wave speed for a transverse wave on this string is 220ms−1 and the string vibrates in three loops. (a) Find the length of the string. (b) If the maximum amplitude of a particle is 0.5 cm, write a suitable equation describing the motion.
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.
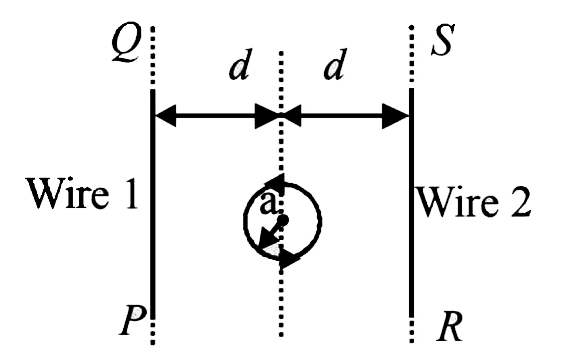
(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop at a height h above the loop is zero. In that case
View SolutionThe figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
.
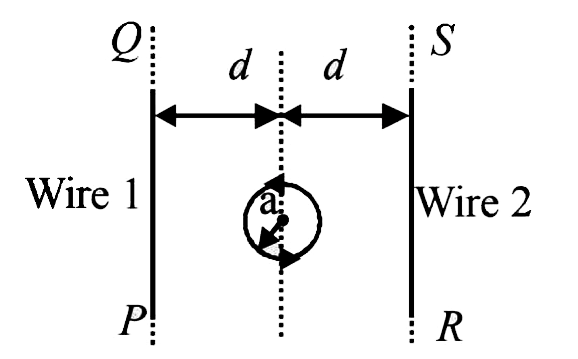
(5) Consider d>>a, and the loop is rotated about its diameter parallel to the wires by 30∘ from the position shown in the figure. If the currents in the wire are in the opposite directions, the torque on the loop at its new position will be ( assume that the net field due to the wires is constant over the loop).
View Solutionin an experiment it was found that string vibrates in n loops when a mass M is placed on the pan. What mass should be placed on the pan to make it vibrate in 2n loops with same frequency ? ( neglect the mass of pan )
View SolutionIn Melde's experiment , when a string is stretched by a piece of glass it vibrates with 7l∞ps . When the glass piece is completely immersed in water the string vibrates in 9l∞ps. What is the specific gravity of glass ?
View SolutionIn Melde's experiment it was found that the string vibrated in 3 loops when 8gm were placed in a pan. What mass must be placed in the pan to make the string vibrate in 5 loops? (Neglect the mass of the string an the pan).
View Solution