A man goes at the top of a smooth inclined plane. He releases a bag to fall freely and himself slides down on inclined plane to reach the bottom. If u1andu2 are the respective velocities of the man and bag at the bottom of inclined plane, then
u1>u2
u1<u2
u1=u2
u1andu2 cannot be compared
The correct Answer is:C
To solve the problem, we need to analyze the motion of both the man sliding down the inclined plane and the bag falling freely. We will use the principle of conservation of energy for both cases.
1. Identify the System:
- We have a man sliding down a smooth inclined plane and a bag falling freely from the same height H.
2. Define Variables:
- Let m1 be the mass of the man and m2 be the mass of the bag.
- Let u1 be the final velocity of the man at the bottom of the incline.
- Let u2 be the final velocity of the bag when it reaches the ground.
3. Energy Conservation for the Man:
- At the top of the incline, the man has potential energy and no kinetic energy (since he starts from rest).
- Initial potential energy of the man: PEinitial=m1gH
- Final potential energy at the bottom: PEfinal=0
- Final kinetic energy of the man: KEfinal=12m1u21
- By conservation of energy:
m1gH=12m1u21
- Cancel m1 from both sides (assuming m1≠0):
gH=12u21
- Rearranging gives:
u21=2gH⇒u1=√2gH
4. Energy Conservation for the Bag:
- The bag also starts from rest and falls freely.
- Initial potential energy of the bag: PEinitial=m2gH
- Final potential energy at the ground: PEfinal=0
- Final kinetic energy of the bag: KEfinal=12m2u22
- By conservation of energy:
m2gH=12m2u22
- Cancel m2 from both sides (assuming m2≠0):
gH=12u22
- Rearranging gives:
u22=2gH⇒u2=√2gH
5. Comparing Velocities:
- From the equations derived:
u1=√2gHandu2=√2gH
- Therefore, we conclude:
u1=u2
Final Relation:
The relation between the velocities of the man and the bag at the bottom of the inclined plane is:
u1=u2
- We have a man sliding down a smooth inclined plane and a bag falling freely from the same height H.
- Let m1 be the mass of the man and m2 be the mass of the bag.
- Let u1 be the final velocity of the man at the bottom of the incline.
- Let u2 be the final velocity of the bag when it reaches the ground.
- At the top of the incline, the man has potential energy and no kinetic energy (since he starts from rest).
- Initial potential energy of the man: PEinitial=m1gH
- Final potential energy at the bottom: PEfinal=0
- Final kinetic energy of the man: KEfinal=12m1u21
- By conservation of energy:
m1gH=12m1u21
- Cancel m1 from both sides (assuming m1≠0):
gH=12u21
- Rearranging gives:
u21=2gH⇒u1=√2gH
- The bag also starts from rest and falls freely.
- Initial potential energy of the bag: PEinitial=m2gH
- Final potential energy at the ground: PEfinal=0
- Final kinetic energy of the bag: KEfinal=12m2u22
- By conservation of energy:
m2gH=12m2u22
- Cancel m2 from both sides (assuming m2≠0):
gH=12u22
- Rearranging gives:
u22=2gH⇒u2=√2gH
- From the equations derived:
u1=√2gHandu2=√2gH
- Therefore, we conclude:
u1=u2
The relation between the velocities of the man and the bag at the bottom of the inclined plane is:
u1=u2
Topper's Solved these Questions
Similar Questions
A disc of mass 3 kg rolls down an inclined plane of height 5 m. The translational kinetic energy of the disc on reaching the bottom of the inclined plane is
View SolutionA block is placed on the top of a plane inclined at 37∘ with horizontal. The length of the plane is 5m. The block slides down the plane and reaches the bottom.
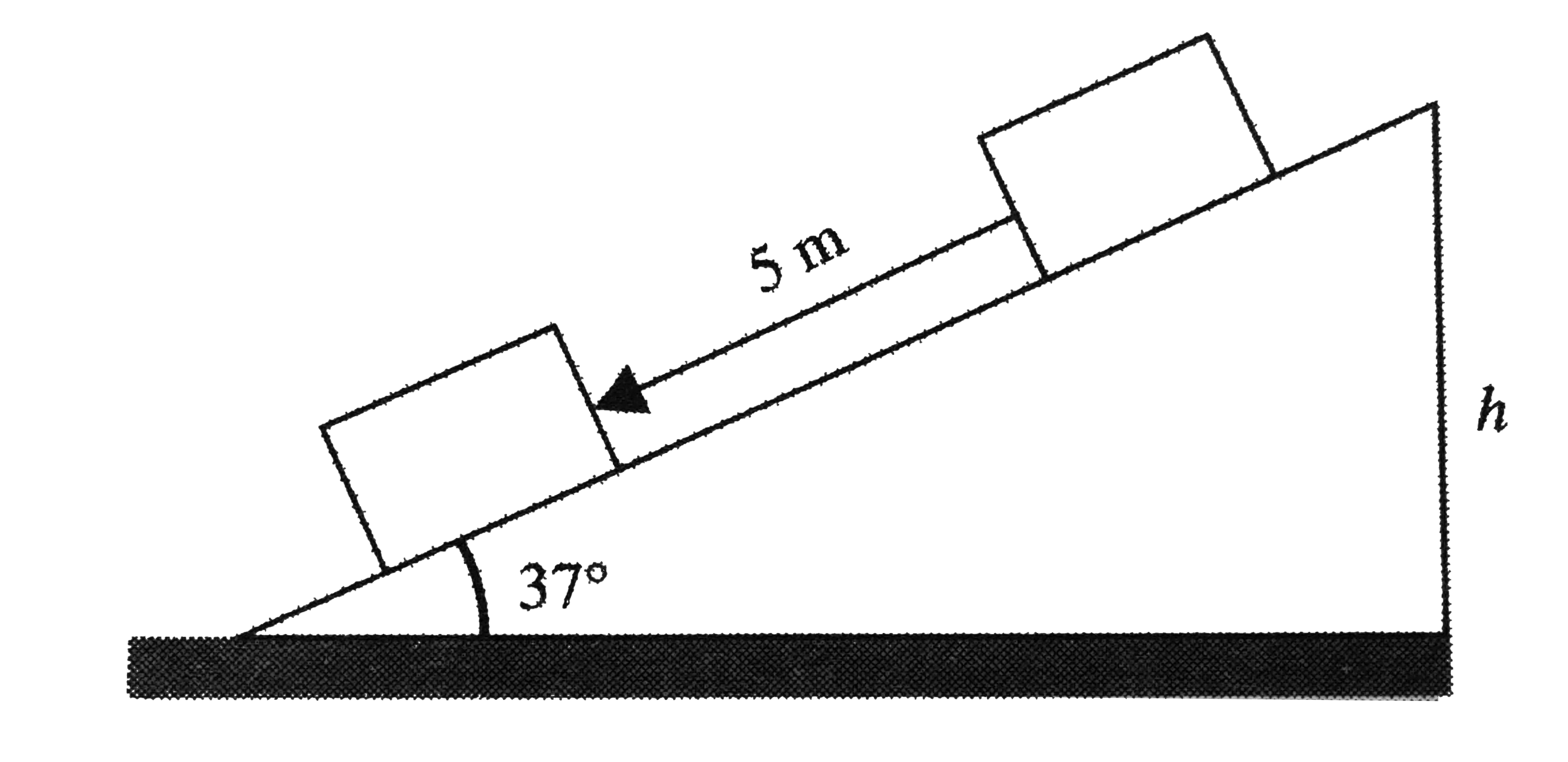
a. Find the speed of the block at the bottom if the inclined plane is smooth.
b. Find the speed of the block at the bottom if the coefficient of friction is 0.25.
View Solution
Knowledge Check
A block released from rest from the top of a smooth inclined plane of angle θ1 reaches the bottom in time t1. The same block released from rest from the top of another smooth inclined plane of angle θ2 reaches the bottom in time t2 If the two inclined planes have the same height, the relation between t1andt2 is
At2t1=(sinθ1sinθ2)1/2Bt2t1=1Ct2t1=sinθ1sinθ2Dt2t1=sin2θ1sin2θ2
A solid cylinder of mass M and radius R rolls down an inclined plane of height h. The angular velocity of the cylinder when it reaches the bottom of the plane will be :
View SolutionA uniform ring rolls down an inclined plane without slipping. If it reaches the bottom of a speed of 2m/s, then calculate the height of the inclined plane (use g=10m/s2)
View SolutionA uniform ring rolls down an inclined plane without slipping. If it reaches the bottom of a speed of 2m/s, then calculate the height of the inclined plane (use g=10m/s2)
View SolutionIf a ring, a disc, a solid sphere and a cyclinder of same radius roll down an inclined plane, the first one to reach the bottom will be:
View SolutionA block of mass m takes time t to slide down on a smooth inclined plane of angle of inclination θ and height h. If same block slids down on a rough inclined plane of same angle of inclination and same height and takes time n times of initial value, then coefficient friction between block and inclined plane is
View SolutionA body is kept on a smooth inclined plane having an inclination of 1 in x. Then,
View SolutionDerive an expression for the acceleration of a body sliding down a rough inclined plane.
View Solution
