A block of mass m takes time t to slide down on a smooth inclined plane of angle of inclination θ and height h. If same block slids down on a rough inclined plane of same angle of inclination and same height and takes time n times of initial value, then coefficient friction between block and inclined plane is
[1+n2]tanθ
[1−1n2]tanθ
[1−n2]tanθ
[1+1n2]tanθ
To solve the problem step by step, we will analyze the motion of the block on both the smooth and rough inclined planes and derive the coefficient of friction.
Step 1: Analyze the smooth inclined plane
1. Identify Forces: On a smooth inclined plane, the only force acting down the incline is the component of gravitational force, which is mgsinθ.
2. Calculate Acceleration: Since there is no friction, the acceleration a of the block is given by:
a=gsinθ
Step 2: Calculate the time taken to slide down the smooth inclined plane
1. Height and Length Relationship: The height h and the length l of the incline are related by:
sinθ=hl⟹l=hsinθ
2. Use Kinematic Equation: The block starts from rest, so we use the equation:
s=ut+12at2⟹l=0+12(gsinθ)t2
Substituting for l:
hsinθ=12(gsinθ)t2
3. Solve for Time t:
t2=2hgsin2θ⟹t=√2hgsin2θ
Step 3: Analyze the rough inclined plane
1. Identify Forces: On the rough inclined plane, the forces acting on the block are:
- Down the incline: mgsinθ
- Up the incline: friction f=μmgcosθ
2. Net Force and Acceleration: The net force acting down the incline is:
ma=mgsinθ−μmgcosθ
Dividing by m:
a=gsinθ−μgcosθ
Step 4: Calculate the time taken to slide down the rough inclined plane
1. Using the same length l:
l=hsinθ
Using the kinematic equation again:
hsinθ=12(gsinθ−μgcosθ)t22
2. Solve for Time t2:
t22=2hgsinθ(1−μcosθsinθ)⟹t2=
⎷2hgsinθ(1−μcosθsinθ)
Step 5: Relate the times t2 and t
1. Given Relation: It is given that t2=nt:
⎷2hgsinθ(1−μcosθsinθ)=n√2hgsin2θ
2. Square Both Sides:
2hgsinθ(1−μcosθsinθ)=n22hgsin2θ
3. Cancel 2h/g:
1sinθ(1−μcosθsinθ)=n21sin2θ
4. Cross Multiply:
sin2θ=n2sinθ(1−μcosθsinθ)
Step 6: Solve for the coefficient of friction μ
1. Rearranging:
sin2θ=n2sinθ−n2μcosθ
2. Isolate μ:
n2μcosθ=n2sinθ−sin2θ
μ=n2sinθ−sin2θn2cosθ
μ=tanθ(1−1n2)
Final Answer
Thus, the coefficient of friction μ between the block and the inclined plane is:
μ=tanθ(1−1n2)
1. Identify Forces: On a smooth inclined plane, the only force acting down the incline is the component of gravitational force, which is mgsinθ.
2. Calculate Acceleration: Since there is no friction, the acceleration a of the block is given by:
a=gsinθ
1. Height and Length Relationship: The height h and the length l of the incline are related by:
sinθ=hl⟹l=hsinθ
2. Use Kinematic Equation: The block starts from rest, so we use the equation:
s=ut+12at2⟹l=0+12(gsinθ)t2
Substituting for l:
hsinθ=12(gsinθ)t2
3. Solve for Time t:
t2=2hgsin2θ⟹t=√2hgsin2θ
1. Identify Forces: On the rough inclined plane, the forces acting on the block are:
- Down the incline: mgsinθ
- Up the incline: friction f=μmgcosθ
2. Net Force and Acceleration: The net force acting down the incline is:
ma=mgsinθ−μmgcosθ
Dividing by m:
a=gsinθ−μgcosθ
1. Using the same length l:
l=hsinθ
Using the kinematic equation again:
hsinθ=12(gsinθ−μgcosθ)t22
2. Solve for Time t2:
t22=2hgsinθ(1−μcosθsinθ)⟹t2=
⎷2hgsinθ(1−μcosθsinθ)
1. Given Relation: It is given that t2=nt:
⎷2hgsinθ(1−μcosθsinθ)=n√2hgsin2θ
2. Square Both Sides:
2hgsinθ(1−μcosθsinθ)=n22hgsin2θ
3. Cancel 2h/g:
1sinθ(1−μcosθsinθ)=n21sin2θ
4. Cross Multiply:
sin2θ=n2sinθ(1−μcosθsinθ)
1. Rearranging:
sin2θ=n2sinθ−n2μcosθ
2. Isolate μ:
n2μcosθ=n2sinθ−sin2θ
μ=n2sinθ−sin2θn2cosθ
μ=tanθ(1−1n2)
Thus, the coefficient of friction μ between the block and the inclined plane is:
μ=tanθ(1−1n2)
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-C)
63 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-A)
65 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
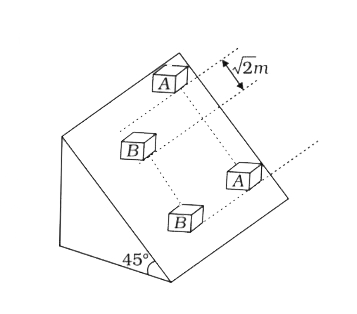
Two identical blocks A and B of equal masses are placed on rough inclined plane as shown in the figure. Initially the block A is √2m behind the block B. Coefficient of kinetic friction for the blocks A and B are 0.2 and 0.3 respectively (g=10m/s2). By the time the two blocks come on the same line on the inclined plane if they are released simultaneously, the distance moved by B is βm Find the value of β
View SolutionA block of mass m slides down a rough inclined plane with an acceleration g2

View Solution
Knowledge Check
Starting from rest, a body slides down a 45∘ inclined plane in twice the time it itakes to slide the same distance in the absence of friction.
They the coefficient of friction between the body and the inclined plane isA1/4B2/3C3/4D√3/2
A block slides down on inclined plane (angle of inclination 60∘ ) with an accelration g/2 Find the coefficient friction

View SolutionA block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.

View SolutionA block moves down a smooth inclined plane of inclination θ. Its velocity on reaching the bottom is v. If it slides down a rough inclined plane of some inclination, its velocity on reaching the bottom is v/n, where n is a number greater than 0. The coefficient of friction is given by -
View SolutionA block of mass m is kept on an inclined plane is angle inclination θ(<ϕ), where ϕ= angle of friction. Then :

View SolutionStarting from rest , a body slides down at 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View Solution
