The current density varies radical distance r as J=ar2, in a cylindrical wire of radius R. The current passing through the wire between radical distance R/3andR/2 is,
65πaR42592
25πaR472
65πa2R32938
81πa2R4144
The correct Answer is:A
To solve the problem of finding the current passing through a cylindrical wire between the radial distances R3 and R2 where the current density J varies with the radial distance r as J=Ar2, we will follow these steps:
Step 1: Understand the Current Density
The current density J is given by the equation:
J=Ar2
where A is a constant and r is the radial distance from the center of the cylindrical wire.
Step 2: Express Current in Terms of Current Density
The current I flowing through a differential area dA can be expressed as:
dI=J⋅dA
For a cylindrical wire, the differential area dA at a distance r is given by the circumference of the circle multiplied by an infinitesimal thickness dr:
dA=2πrdr
Thus, we can write:
dI=J⋅dA=Ar2⋅(2πrdr)=2πAr3dr
Step 3: Integrate to Find Total Current
To find the total current I flowing through the wire between the limits r=R3 and r=R2, we need to integrate dI:
I=∫R/2R/32πAr3dr
Step 4: Perform the Integration
The integral can be computed as follows:
I=2πA∫R/2R/3r3dr
The integral of r3 is:
∫r3dr=r44
Thus, we have:
I=2πA(r44)R/2R/3
Substituting the limits:
I=2πA((R/2)44−(R/3)44)
Calculating the terms:
I=2πA(R464−R4324)⋅14
I=πAR48(164−1324)
Step 5: Simplify the Expression
To simplify 164−1324:
Finding a common denominator (which is 64×324=20736):
164=32420736,1324=6420736
Thus:
164−1324=324−6420736=26020736
Now substituting back:
I=πAR48⋅26020736
I=260πAR4165888
Final Result
Thus, the current passing through the wire between the radial distances R3 and R2 is:
I=65πAR441472
The current density J is given by the equation:
J=Ar2
where A is a constant and r is the radial distance from the center of the cylindrical wire.
The current I flowing through a differential area dA can be expressed as:
dI=J⋅dA
For a cylindrical wire, the differential area dA at a distance r is given by the circumference of the circle multiplied by an infinitesimal thickness dr:
dA=2πrdr
Thus, we can write:
dI=J⋅dA=Ar2⋅(2πrdr)=2πAr3dr
To find the total current I flowing through the wire between the limits r=R3 and r=R2, we need to integrate dI:
I=∫R/2R/32πAr3dr
The integral can be computed as follows:
I=2πA∫R/2R/3r3dr
The integral of r3 is:
∫r3dr=r44
Thus, we have:
I=2πA(r44)R/2R/3
Substituting the limits:
I=2πA((R/2)44−(R/3)44)
Calculating the terms:
I=2πA(R464−R4324)⋅14
I=πAR48(164−1324)
To simplify 164−1324:
Finding a common denominator (which is 64×324=20736):
164=32420736,1324=6420736
Thus:
164−1324=324−6420736=26020736
Now substituting back:
I=πAR48⋅26020736
I=260πAR4165888
Thus, the current passing through the wire between the radial distances R3 and R2 is:
I=65πAR441472
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - DRIFT OF ELECTRONS2videos
CURRENT ELECTRICITY
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - LIMITATIONS OF OHM S LAW4videos
CURRENT ELECTRICITY
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ELECTRIC CURRENT IN CONDUCTORS2videos
CURRENT ELECTRICITY
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - Assertion And Reason30videos
COMMUNITCATION SYSTEMS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason15videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
In the figure shown the current flowing through 2R is:
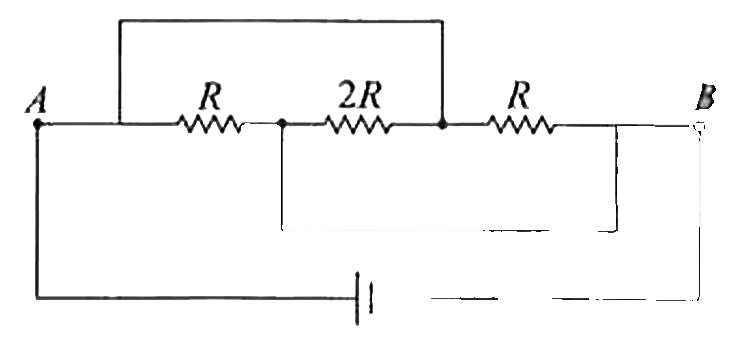 View Solution
View SolutionThe current density in a wire of radius a varies with radial distance r as J=J0r2a, where J0 is a constant. Choose the incorrect statement.
View SolutionElectric current is passing unfiormly through a solid cylinderical wire of radius R. The current I passing through circular cross-section of radius r measured from the axis of the cylinder (r<R) varies as shown in
View SolutionThe current density ¯¯¯J inside a long, solid cylindrical wire of radius a=12mm is in the direction of the central axis, and its magnitude varies linearly with radial distance r from the axis according to J=J0ra, where J0=1054πA/m2. Find the magnitude of the magnetic field at r=a2 in μT
View SolutionThe current density ¯¯¯J inside a long, solid cylindrical wire of radius a=12mm is in the direction of the central axis, and its magnitude varies linearly with radial distance r from the axis according to J=J0ra, where J0=1054πA/m2. Find the magnitude of the magnetic field at r=a2 in μT
View SolutionA long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J=kr2, where, k is a constant. Find an expression for the magnetic field B at a distance r(<R) from the axis
 View Solution
View SolutionConsider the circuit shown in fig.
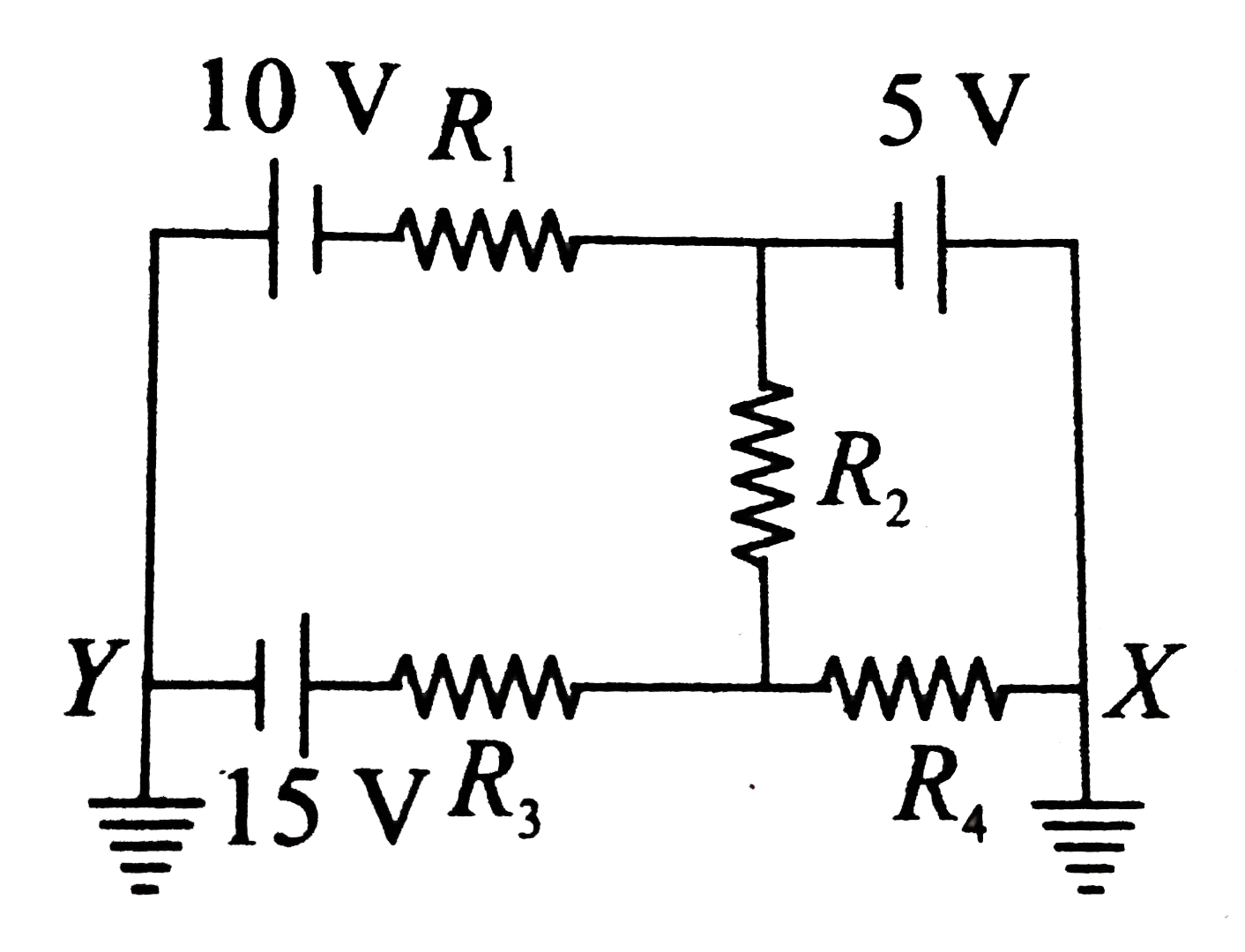
Assuming R1=2Ω, current passing through resistance R1 isView SolutionThe current density across a cylindrical conductor of radius R varies in magnitude according to the equation J=J0(1−rR) where r is the distance from the central axis. Thus, the current density is a maximum J0 at that axis (r = 0) and decreases linearly to zero at the surface (r = R). Calculate the current in terms of J0 and the conductor 's cross - sectional area A=πR2.
View SolutionA:Current density is a very is a vector quantity .
R : Electric current , passing through a given unit area is current density.View SolutionA cylindrical wire of radius R has current density varying with distance r form its axis as J(x)=J0(1−r2R2) . The total current through the wire is
View Solution

