In LCR - circuit if resistance increases, quality factor
increases finitely
decreases finitely
remains constant
None of these
The correct Answer is:B
To solve the problem regarding the change in the quality factor (Q) of an LCR circuit when the resistance (R) increases, we can follow these steps:
1. Understand the Quality Factor Formula:
The quality factor (Q) of an LCR circuit is given by the formula:
Q=ω0LR
where:
- ω0 is the angular frequency,
- L is the inductance,
- R is the resistance.
2. Analyze the Effect of Increasing Resistance:
From the formula, we can see that Q is directly proportional to the inductance L and the angular frequency ω0, and inversely proportional to the resistance R.
3. Determine the Relationship:
If the resistance R increases, the denominator of the fraction increases. Since Q is inversely proportional to R, this means that as R increases, Q must decrease.
4. Conclusion on Quality Factor Change:
Therefore, when resistance increases, the quality factor Q decreases. However, it is important to note that this decrease is finite; it cannot decrease infinitely because ω0L remains constant in the equation.
5. Final Answer:
The quality factor decreases finitely when the resistance increases.
The quality factor (Q) of an LCR circuit is given by the formula:
Q=ω0LR
where:
- ω0 is the angular frequency,
- L is the inductance,
- R is the resistance.
From the formula, we can see that Q is directly proportional to the inductance L and the angular frequency ω0, and inversely proportional to the resistance R.
If the resistance R increases, the denominator of the fraction increases. Since Q is inversely proportional to R, this means that as R increases, Q must decrease.
Therefore, when resistance increases, the quality factor Q decreases. However, it is important to note that this decrease is finite; it cannot decrease infinitely because ω0L remains constant in the equation.
The quality factor decreases finitely when the resistance increases.
Topper's Solved these Questions
Similar Questions
In LCR circuit during resonance
View SolutionIn series LCR circuit at resonance
View SolutionThe value of quality factor is:
View SolutionThe figure shows a series LCR circuit connected to a varriable of 200 V source with L=50 mH, C=80μF and R=40Ω find.
(i) the source frequency which drives the circuit in resonance,
(ii) the quality factor (Q) of the circuit.
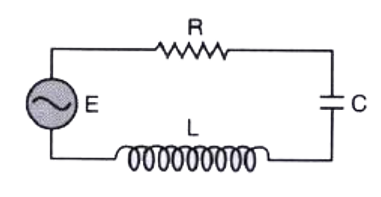 View Solution
View SolutionIn LCR circuit as shown in figure
 View Solution
View SolutionA : A series resonant circuit is also known as an acceptor circuit.
R : For large value of Ohmic resistance, the quality factor of a series resonant circuit is high.View SolutionA wire of reistance R is connected in series with an inductor of reactance ω L. Then quality factor of RL circuit is
View SolutionAnswer the following:
(a) What do you understand by 'sharpness of resonance' for a series LCR resonant circuit? How is it related with the quality factor 'Q' of the circuit? Using the graphs given in the diagram, explain the factors which affect it. For which graph is the resistance (R ) minimum?
(b) A 2μF capacitor, 100Ω resistor and 8H inductor are connected in series with an ac source. Find the frequency of the ac source for which the current drawn in the circuit is maximum.
If the peak value of emf of the source is 200 V, calculate the (i) maximum current, and (ii) inductive and capacitive reactance of the circuit at resonance.
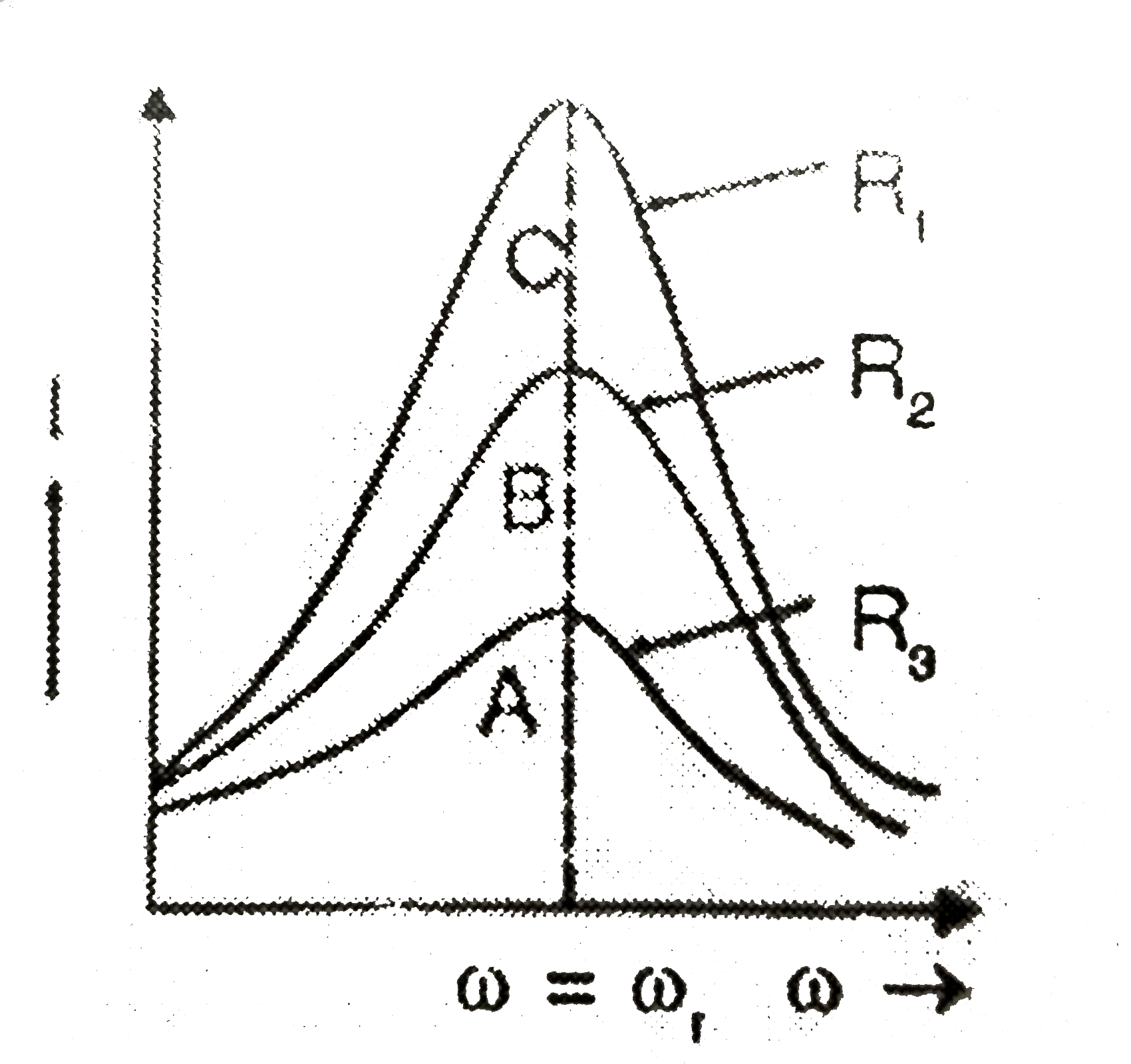 View Solution
View SolutionThe quality factor of LCR circuit having resistance ( R ) and inductance ( L ) at resonance frequency (ω) is given by
View SolutionA series LCR circuit, has equal resistance capacitive reactance. What is the phase angle between voltage across generator and resistor ?
View Solution
