The self inductance of a solenoid that has a cross-sectional area of 1cm2, a length of 10 cm and 1000 turns of wire is
0.86mH
1.06mH
1.26mH
1.46mH
The correct Answer is:C
To calculate the self-inductance L of a solenoid, we can use the formula:
L=μ0⋅N2⋅Al
where:
- μ0 is the permeability of free space, approximately 4π×10−7H/m
- N is the total number of turns of the solenoid
- A is the cross-sectional area of the solenoid in square meters
- l is the length of the solenoid in meters
1. Identify the given values:
- Cross-sectional area A=1cm2=1×10−4m2
- Length l=10cm=0.1m
- Number of turns N=1000
2. Substitute the values into the formula:
L=μ0⋅N2⋅Al
3. Calculate N2:
N2=10002=1000000
4. Substitute μ0, N2, A, and l into the equation:
L=(4π×10−7)⋅(1000000)⋅1×10−40.1
5. Simplify the expression:
L=(4π×10−7)⋅(1000000)⋅(10−3)
L=4π×10−4H
6. Calculate 4π:
4π≈12.5664
7. Final calculation:
L≈12.5664×10−4H=1.25664×10−3H
L≈1.26mH
Final Answer:
The self-inductance of the solenoid is approximately 1.26mH.
- μ0 is the permeability of free space, approximately 4π×10−7H/m
- N is the total number of turns of the solenoid
- A is the cross-sectional area of the solenoid in square meters
- l is the length of the solenoid in meters
- Cross-sectional area A=1cm2=1×10−4m2
- Length l=10cm=0.1m
- Number of turns N=1000
L=μ0⋅N2⋅Al
N2=10002=1000000
L=(4π×10−7)⋅(1000000)⋅1×10−40.1
L=(4π×10−7)⋅(1000000)⋅(10−3)
L=4π×10−4H
4π≈12.5664
L≈12.5664×10−4H=1.25664×10−3H
L≈1.26mH
The self-inductance of the solenoid is approximately 1.26mH.
Topper's Solved these Questions
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Papper 3
50 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 1
50 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 3
50 Videos
- NUCLEIBOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason
15 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - NCERT Exemplar
11 Videos
Similar Questions
Derive the expression for the self inductance of a long solenoid of cross sectional area A and length l, having n turns per unit length.
View SolutionThe self inductance of a solenoid of length L, area of cross-section A and having N turns is-
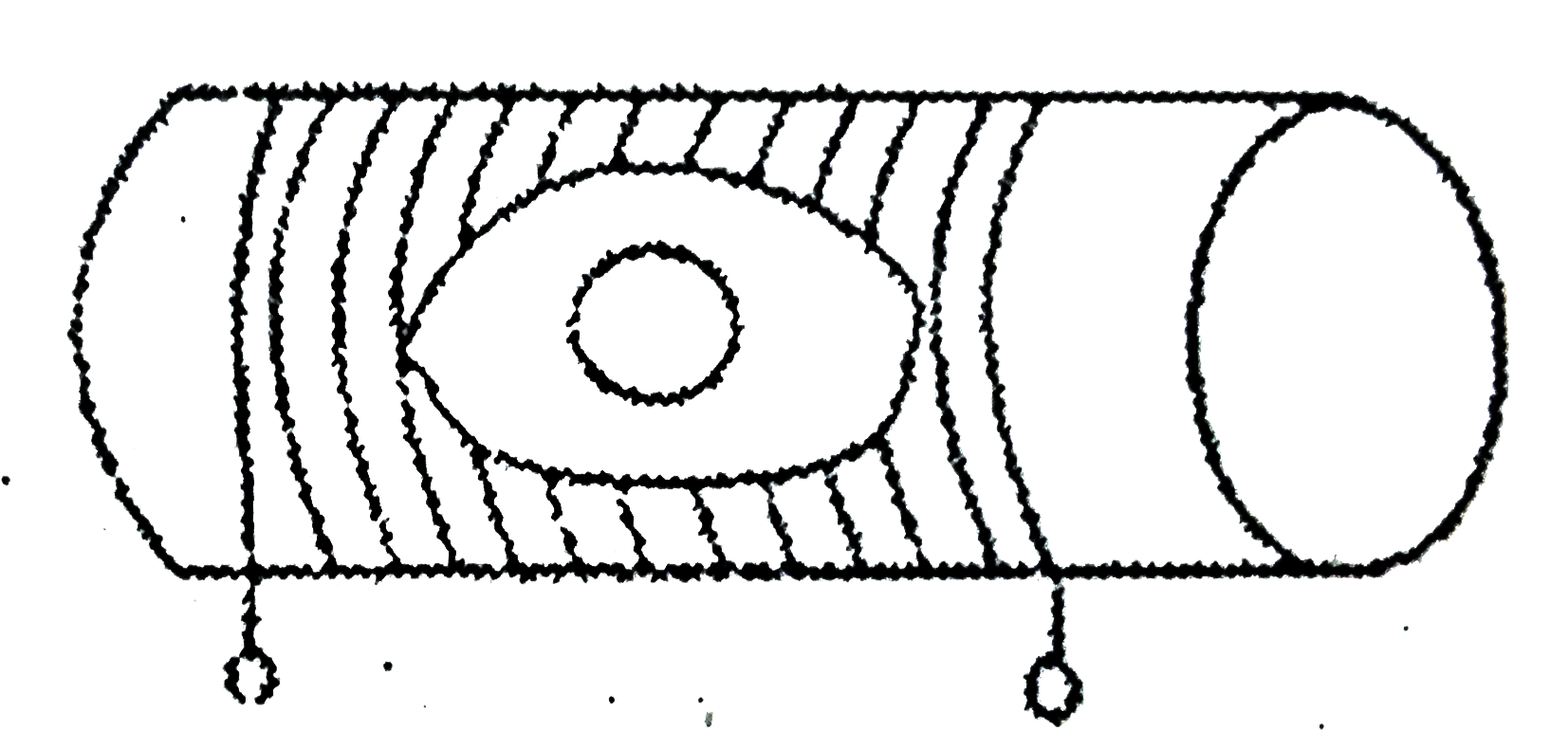
View SolutionA circular coil with a cross-sectional area of 4cm2 has 10 turns. It is placed at the center of a long solenoid that has 15 turns/cm and a cross sectional area of 10cm2, shown in the figure. The axis of the coil conicides with the axis of the solenoid. What is their mutual inductance?
View SolutionThe self inductance L of a solenoid of length l and area of cross-section A, with a fixed number of turns N increases as
View SolutionThe self inductance L of a solenoid of length l and area of cross-section A, with a fixed number of turns N increases as
View SolutionThe self inductance L of a solenoid of length l and area of cross-section A, with a fixed number of turns N increases as
View SolutionA solenoid of length 20cm, area of cross- section 4.0cm2 and having 4000 turns is placed inside another solenoid of 2000 turns having a cross - sectional area 8.0cm2 and length 10cm. Find the mutual inductance between the solenoids.
View SolutionThe self inductance L of a solenoid depends on the number of turns per unit length 'n' as
View SolutionTwo coaxial solenoids are made by winding thin insulated wire over a pipe of cross-sectional area A=10cm2 and length =10cm. If one of the solenoid has 300 turns and the other 400 turns, their mutual indcutance is
View Solution(a) Define self inductance. Write its S.I. units
(b) Derive and expression for self inductance of a long solenoid of length l cross-sectional area A having N number of turns.
View Solution
