In an experiment to find focal length of a concave mirror, a graph is drawn between the magnitudes of (u) and (v). The graph looks like.
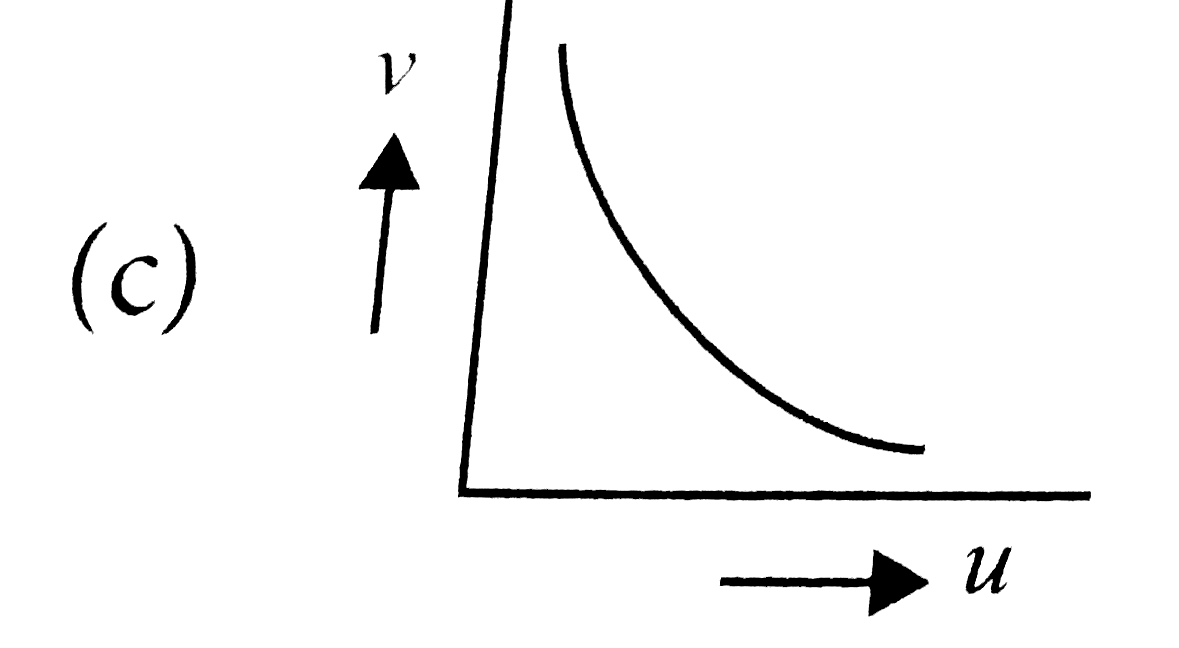

The correct Answer is:C
To solve the problem of determining the correct graph between the magnitudes of object distance (u) and image distance (v) for a concave mirror, we can follow these steps:
1. Understanding the Mirror Formula:
The mirror formula for a concave mirror is given by:
1f=1u+1v
where f is the focal length, u is the object distance, and v is the image distance.
2. Rearranging the Formula:
We can rearrange the mirror formula to express u in terms of v:
1u=1f−1v
This can be rewritten as:
u=fvv−f
3. Differentiating the Equation:
To analyze the relationship between u and v, we differentiate both sides:
dudv=ddv(fvv−f)
Using the quotient rule, we find:
dudv=f(v−f)−fv(v−f)2=−f2(v−f)2
4. Analyzing the Slope:
The derivative dudv is negative, indicating that as v increases, u decreases. This means the graph of u versus v will have a negative slope.
5. Identifying the Graph:
Since the relationship is non-linear (as indicated by the squared term in the denominator), the graph will not be a straight line. Therefore, we look for a graph that shows a decreasing trend that is not linear.
6. Conclusion:
Based on the analysis, the correct graph that represents the relationship between the magnitudes of u and v for a concave mirror is the one that shows a decreasing curve. From the options provided, we conclude that option C is the correct answer.
The mirror formula for a concave mirror is given by:
1f=1u+1v
where f is the focal length, u is the object distance, and v is the image distance.
We can rearrange the mirror formula to express u in terms of v:
1u=1f−1v
This can be rewritten as:
u=fvv−f
To analyze the relationship between u and v, we differentiate both sides:
dudv=ddv(fvv−f)
Using the quotient rule, we find:
dudv=f(v−f)−fv(v−f)2=−f2(v−f)2
The derivative dudv is negative, indicating that as v increases, u decreases. This means the graph of u versus v will have a negative slope.
Since the relationship is non-linear (as indicated by the squared term in the denominator), the graph will not be a straight line. Therefore, we look for a graph that shows a decreasing trend that is not linear.
Based on the analysis, the correct graph that represents the relationship between the magnitudes of u and v for a concave mirror is the one that shows a decreasing curve. From the options provided, we conclude that option C is the correct answer.
Topper's Solved these Questions
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 1
50 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 2
50 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Papper 2
50 Videos
- NUCLEIBOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason
15 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - NCERT Exemplar
11 Videos
Similar Questions
Focal length of a concave mirror is
View SolutionIn the experiment to determine the focal length of a concave mirror by graphical methods the u - v graph is
View SolutionWhat is the focal length of a concave mirror of radius of curvature 16.0 cm?
View SolutionThe focal length of a concave mirror is 10 cm. Find its radius of curvature.
View SolutionIn an experiment to measure the focal length of a concave mirror. If was found that for an object distance of 0.30 m, the image distance come out to be 0.60 m. Let us determine the focal length.
View SolutionIn u−v method to find focal length of a concave mirror, if object distance is found to be 10.0cm and image distance was also found to be 10.0cm, then find maximum permissible error in (f).
View SolutionThe graph between 1v and 1u for a concave mirror looks like.
View SolutionThe graph between 1v and 1u for a concave mirror looks like.
View SolutionAn object is placed midway between a concave mirror of focal length f and a convex mirror of focal length f. The distance between the two mirrors is 6f. Trace the ray that is first incident on the concave mirror and then the convex mirror.
View SolutionFor a concave mirrorr, if real image is formed the graph between 1u and 1v is of the form
View Solution
