A proton has kinetic energy E = 100 keV which is equal to that of a photon. The wavelength of photon is and that of proton is . The ratio of is proportional to
The correct Answer is:D
To solve the problem, we need to find the ratio of the wavelengths of a photon and a proton given that the kinetic energy of the proton is equal to the energy of the photon.
1. Identify the Energy of the Photon:
The energy of the photon E is given as 100keV. We can express this in joules:
E=100keV=100×1.6×10−19J=1.6×10−14J
2. Calculate the Wavelength of the Photon (λ2):
The wavelength of the photon can be calculated using the formula:
λ2=hcE
where h is Planck's constant (6.626×10−34Js) and c is the speed of light (3×108m/s).
Substituting the values:
λ2=(6.626×10−34)(3×108)1.6×10−14≈1.24×10−6m
3. Calculate the Wavelength of the Proton (λ1):
The momentum p of the proton can be related to its kinetic energy E using:
E=p22m
Rearranging gives:
p=√2mE
The wavelength of the proton is given by:
λ1=hp=h√2mE
Substituting the values:
λ1=h√2m⋅1.6×10−14
Here, the mass of the proton m≈1.67×10−27kg.
4. Calculate the Ratio of Wavelengths (λ2λ1):
Now we can find the ratio:
λ2λ1=hcEh√2mE=hc√2mEE
Simplifying gives:
λ2λ1=hc√2mE1/2
Since h and c are constants, we can express the ratio as:
λ2λ1∝√2mE−1/2
5. Final Result:
Therefore, the ratio λ2λ1 is proportional to E−1/2.
The energy of the photon E is given as 100keV. We can express this in joules:
E=100keV=100×1.6×10−19J=1.6×10−14J
The wavelength of the photon can be calculated using the formula:
λ2=hcE
where h is Planck's constant (6.626×10−34Js) and c is the speed of light (3×108m/s).
Substituting the values:
λ2=(6.626×10−34)(3×108)1.6×10−14≈1.24×10−6m
The momentum p of the proton can be related to its kinetic energy E using:
E=p22m
Rearranging gives:
p=√2mE
The wavelength of the proton is given by:
λ1=hp=h√2mE
Substituting the values:
λ1=h√2m⋅1.6×10−14
Here, the mass of the proton m≈1.67×10−27kg.
Now we can find the ratio:
λ2λ1=hcEh√2mE=hc√2mEE
Simplifying gives:
λ2λ1=hc√2mE1/2
Since h and c are constants, we can express the ratio as:
λ2λ1∝√2mE−1/2
Therefore, the ratio λ2λ1 is proportional to E−1/2.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 150videos
PRACTICE PAPPER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 250videos
PRACTICE PAPPER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Papper 250videos
PRACTICE PAPPER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason15videos
NUCLEI
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - NCERT Exemplar11videos
RAY OPTICS AND OPTICAL INSTRUMENTS
Similar Questions
The energy of a photon is equal to the kinetic energy of a
proton. The energy of the photon is E. Let λ1be the de-Broglie wavelength of the
proton and λ2 be the wavelength of the photon. The ratio λ1λ2 is proportional to
(a)E0 (b) E1/2 (c ) E−1 (d)E−2View SolutionA photelectric material having work-function ϕ0 is illuminated with light of wavelength λ(λ<hcλ0). The fastest photoelectron has a de Broglie wevelength λd. A change in wavelength of the incident light by Δλ results in a change Δλd in λd. Then the ratio Δλd/Δλ is proportional to
View Solution
Knowledge Check
- Question 1 - Select One
The potential energy of particle of mass m varies as
U(x)={E0for0≤x≤10 for >1
The de Broglie wavelength of the particle in the range 0≤x≤1 is λ1 and that in the range x>1 is λ2.
If the total of the particle is 2E0, find λ1/λ2.A√2B√3C√12D√23
Electron are accelerated through a potential difference V and protons are accelerated through a potential difference of 4 V. The de-Broglie wavelength are λeandλp for electrons and protons, respectively The ratio of λeλp is given by ( given , me is mass of electron and mp is mass of proton )
View SolutionThe wavelength of the first Lyman lines of hydrogen He+ and Li2+ ions and λ1,λ2&λ3 the ratio of these wavelengths is
View SolutionA radioactive nucleus can decay be either emitting an α particle or by emitting a β particle. Probability of α decay is 75% while that of β decay is 25% the decayconstatnt of α decay is λ1 and that of β decay is λ2 is λ1λ2
View SolutionThe kinetic energy of the most energetic photoelectrons emitted from a metal surface is doubled when the wavelength of the incident radiation is reduced from λ1 to λ2 The work function of the metal is
View SolutionWhich graph shows how the energy E of a photon of light is related to its wavelengths (λ)?
View SolutionIf λ1 and λ2 denote the wavelength of de Broglie waves for electrons in the first and second Bohr orbits in a hydrogen atom, the λ1λ2 is equal to
View Solution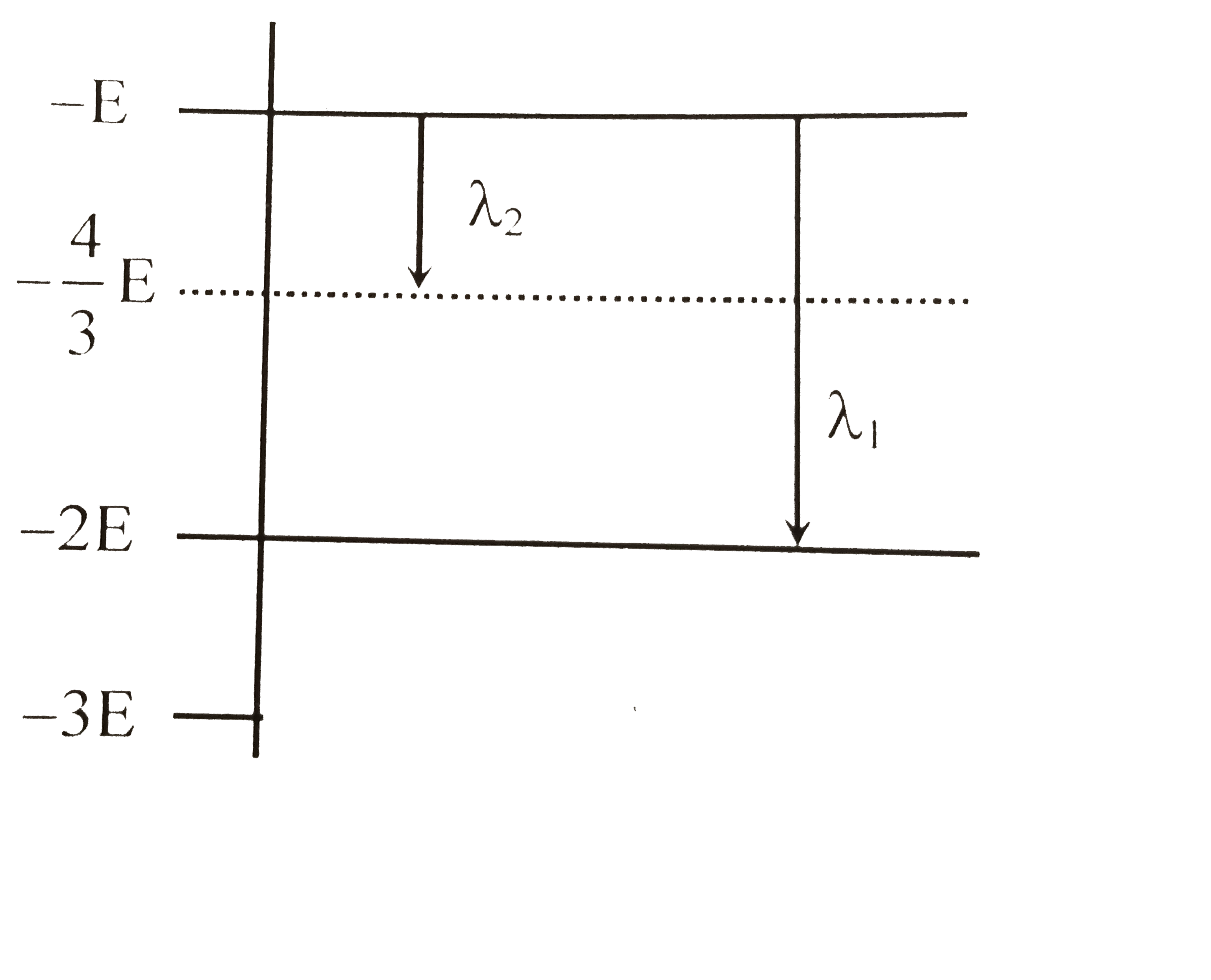
Some energy levels of a molecule are shown in the figure. The ratio of the wavelength r=λ1λ2,is given by:View Solution

