A body falling freely under gravity passes two points 30 m apart in 1 s. From what point above the upper point it began to fall? (Take g = 9.8ms−2).
a. 32.1 m
b. 16.0 m
c. 8.6 m
d. 4.0 m
The correct Answer is:A
To solve the problem, we need to determine the height from which the body fell above the upper point (point A) after passing two points that are 30 meters apart in 1 second. We will use the equations of motion under uniform acceleration due to gravity.
1. Identify the Known Values:
- Distance between points A and B, sAB=30m
- Time taken to travel from A to B, tAB=1s
- Acceleration due to gravity, g=9.8m/s2
2. Define Variables:
- Let s1 be the distance from the initial point to point A.
- Let s2 be the distance from the initial point to point B.
- The relationship between s1 and s2 can be expressed as:
s2−s1=30m
3. Use the Equation of Motion:
- For the distance s1 (from the initial point to point A):
s1=ut+12gt2
Since the body starts from rest, u=0:
s1=12gt2
- For the distance s2 (from the initial point to point B), we need to consider the time taken to reach point B:
s2=u(t+1)+12g(t+1)2
Again, since u=0:
s2=12g(t+1)2
4. Set Up the Equation:
- Substitute s1 and s2 into the distance equation:
s2−s1=30
This gives:
12g(t+1)2−12gt2=30
5. Simplify the Equation:
- Factor out 12g:
12g((t+1)2−t2)=30
- Expand (t+1)2:
(t2+2t+1)−t2=2t+1
- Thus, we have:
12g(2t+1)=30
6. Solve for t:
- Substitute g=9.8:
12⋅9.8(2t+1)=30
4.9(2t+1)=30
2t+1=304.9≈6.12
2t=6.12−1≈5.12
t≈2.56s
7. Calculate s1:
- Now substitute t back into the equation for s1:
s1=12gt2=12⋅9.8⋅(2.56)2
s1≈12⋅9.8⋅6.5536≈32.1m
8. Final Answer:
- The height from which the body began to fall above point A is approximately 32.1 meters.
- Distance between points A and B, sAB=30m
- Time taken to travel from A to B, tAB=1s
- Acceleration due to gravity, g=9.8m/s2
- Let s1 be the distance from the initial point to point A.
- Let s2 be the distance from the initial point to point B.
- The relationship between s1 and s2 can be expressed as:
s2−s1=30m
- For the distance s1 (from the initial point to point A):
s1=ut+12gt2
Since the body starts from rest, u=0:
s1=12gt2
s2=u(t+1)+12g(t+1)2
Again, since u=0:
s2=12g(t+1)2
- Substitute s1 and s2 into the distance equation:
s2−s1=30
This gives:
12g(t+1)2−12gt2=30
- Factor out 12g:
12g((t+1)2−t2)=30
- Expand (t+1)2:
(t2+2t+1)−t2=2t+1
- Thus, we have:
12g(2t+1)=30
- Substitute g=9.8:
12⋅9.8(2t+1)=30
4.9(2t+1)=30
2t+1=304.9≈6.12
2t=6.12−1≈5.12
t≈2.56s
- Now substitute t back into the equation for s1:
s1=12gt2=12⋅9.8⋅(2.56)2
s1≈12⋅9.8⋅6.5536≈32.1m
- The height from which the body began to fall above point A is approximately 32.1 meters.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - RELATIVE VELOCITY18videos
MOTION IN A STRAIGHT LINE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - HOTS10videos
MOTION IN A STRAIGHT LINE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ACCELERATION19videos
MOTION IN A STRAIGHT LINE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason15videos
MOTION IN A PLANE
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion And Reason15videos
OSCILLATIONS
Similar Questions
A body is dropped freely under gravity from the top of a tower of height 78.4 m. Calculate : (i) the time to reach the ground .
Take g = 9.8 ms−2.View SolutionA body is dropped freely under gravity from the top of a tower of height 78.4 m. Calculate : the velocity with which it strikes the ground.
Take g = 9.8 ms−2.View SolutionCalculate the weight of a body of mass 10 kg in kgf . Take g=9.8m s−2 .
View SolutionA body of mass 1 kg falls from a height of 5 m How mcuh energy does it posses at any instant ?(Take g=9.8 m s−2)
View SolutionCalculate the weight of a body of mass 10 kg in newton . Take g=9.8m s−2 .
View SolutionA body falls freely under gravity from rest. Name the kind of energy it will possess
(a) at the point from where it falls,
(b) while falling,
(c) on reaching the ground.View SolutionState the magnitude and direction of the force of gravity acting on a body of mass 5 kg. Take g=9.8ms−2
View SolutionFind the horizontal velocity of the particle when it reach the point Q. Assume the block to be frictionless. Take g=9.8m/s2.
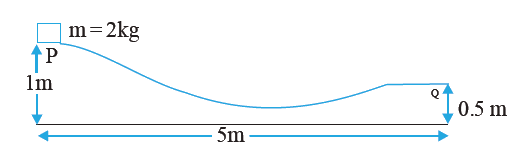 View Solution
View SolutionA body falls from the top of a building and reaches the ground 2.5 s later. How high is the building ? (Take g = 9.8 ms−2)
View SolutionAn aeroplane is flying in a horizontal direction with a velocity of 900 km/h and at a height of 1960m. When it is vertically above the point A on the ground, a body is dropped from it. The body strikes the ground at point B. The distance AB will be (take g=9.8m/s2)
View Solution

