Two town A and B are connected by a regular bus service with a bus leaving in either direction every T minutes. A man leaving in either direction every in the direction A to B notices that a bus goes past him every 18 min in the direction of his motion, and every 6 min in the opposite direction. The period T of the bus service is
4.5 min
9 min
1.2 min
24 min
The correct Answer is:B
To solve the problem, we need to analyze the situation involving the buses and the man traveling between towns A and B. Let's break it down step by step.
Step 1: Define Variables
Let:
- Vm = speed of the man (in km/min)
- Vb = speed of the bus (in km/min)
- T = time interval between buses (in minutes)
Step 2: Understand the Given Information
The man notices:
- A bus passes him every 18 minutes in the direction of his motion (from A to B).
- A bus passes him every 6 minutes in the opposite direction (from B to A).
Step 3: Set Up Equations
When the man is moving from A to B:
- The relative speed of the bus with respect to the man is Vb−Vm.
- The time taken for the bus to pass him is 18 minutes, so:
TVb−Vm=18(1)
When the man is moving from B to A:
- The relative speed of the bus with respect to the man is Vb+Vm.
- The time taken for the bus to pass him is 6 minutes, so:
TVb+Vm=6(2)
Step 4: Rearranging the Equations
From equation (1):
T=18(Vb−Vm)(3)
From equation (2):
T=6(Vb+Vm)(4)
Step 5: Equate the Two Expressions for T
Setting equations (3) and (4) equal to each other:
18(Vb−Vm)=6(Vb+Vm)
Step 6: Simplify the Equation
Expanding both sides:
18Vb−18Vm=6Vb+6Vm
Rearranging gives:
18Vb−6Vb=18Vm+6Vm
12Vb=24Vm
Vb=2Vm(5)
Step 7: Substitute V_b Back into One of the Equations
Substituting equation (5) into equation (3):
T=18(2Vm−Vm)=18Vm
Step 8: Find the Value of T
If we assume the speed of the man Vm is a known value (for example, 1 km/min), we can calculate T:
T=18×1=18 minutes
However, we need to ensure the value of Vm is consistent with the other information provided.
Step 9: Final Calculation
If we assume Vm=20 km/h, we convert it to km/min:
Vm=2060=13 km/min
Then substituting back:
T=18×13=6 minutes
Conclusion
The period T of the bus service is 6 minutes.
Let:
- Vm = speed of the man (in km/min)
- Vb = speed of the bus (in km/min)
- T = time interval between buses (in minutes)
The man notices:
- A bus passes him every 18 minutes in the direction of his motion (from A to B).
- A bus passes him every 6 minutes in the opposite direction (from B to A).
When the man is moving from A to B:
- The relative speed of the bus with respect to the man is Vb−Vm.
- The time taken for the bus to pass him is 18 minutes, so:
TVb−Vm=18(1)
- The relative speed of the bus with respect to the man is Vb+Vm.
- The time taken for the bus to pass him is 6 minutes, so:
TVb+Vm=6(2)
From equation (1):
T=18(Vb−Vm)(3)
T=6(Vb+Vm)(4)
Setting equations (3) and (4) equal to each other:
18(Vb−Vm)=6(Vb+Vm)
Expanding both sides:
18Vb−18Vm=6Vb+6Vm
Rearranging gives:
18Vb−6Vb=18Vm+6Vm
12Vb=24Vm
Vb=2Vm(5)
Substituting equation (5) into equation (3):
T=18(2Vm−Vm)=18Vm
If we assume the speed of the man Vm is a known value (for example, 1 km/min), we can calculate T:
T=18×1=18 minutes
If we assume Vm=20 km/h, we convert it to km/min:
Vm=2060=13 km/min
Then substituting back:
T=18×13=6 minutes
The period T of the bus service is 6 minutes.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - HOTS
10 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT EXEMPLAR PROBLEMS
6 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - KINEMATIC EQUATIONS FOR UNIFORMLY ACCELERATED MOTION
32 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Two towns A and B are connected by a regular bus service with a bus leaving in either direction every T min. A man cycling with a speed of 20kmh−1 in the direction A to B notices that a bus goes past him every 18min in the direction of his motion, and every 6min in the opposite direction. What is the period T of the bus service and with what speed (assumed constant )do the buses ply on the road?
View SolutionTwo cities AandB are connected by a regular bus service with buses plying in either direction every T seconds. The speed of each bus is uniform and equal to Vb. A cyclist cycles from A→B with a uniform speed of Vc. A bus goes past the cyclist in T1 second in the direction A→B and every T2 second in the direction B→A. Then
View SolutionConsider two cities P and Q between which consistent bus servece is available in both directions every x mimutes. A morning jogger is jogging towards Q from P wigh a speed of 10kmh−1. Every 18mim a bus crosses this jogger in its own direction of motion and every 6min another bus crosses in opposite direction. What is time preriod between two consecutive buses and also find the speed of buses ?.
View SolutionTwo particles A and B get 4m closer each second while traveling in opposite direction They get 0.4 m closer every second while traveling in same direction. The speeds of A and B are respectively :
View SolutionA current of 2 A enters at the corner d of a square frame abcd of side 20 cm and leaves at the opposite corner b. A magnetic field B= 0.1 T exists in the space in a direction perpenducular to the plane of the frame as shown in Find the magnitude and direction of the magnetic forces on the four sides of the frame.

View SolutionA water surface is moving at a speed of 15m/s. When he is surfing in the direction of wave, he swing upwards every 0.8 s because of wave crests. While surfing in opposite direction to that of wave motion, he swings upwards every 0.6 s. determine the wavelength of transverse component of the water wave.
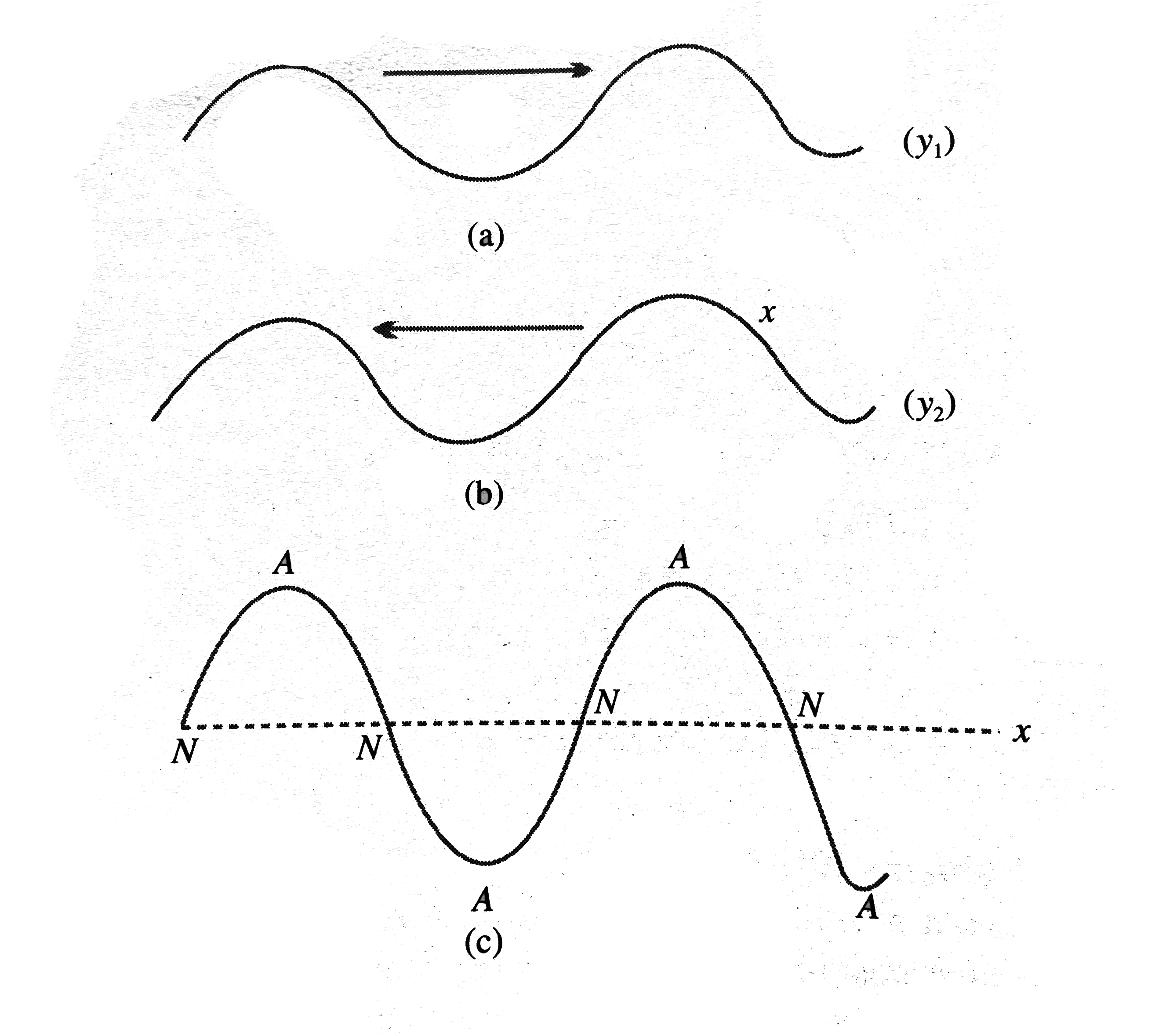
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Amplitude of simple harmonic motion of a point on the string that is located at x=1.8cm will be
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Figure 7.104( c) shows the standing wave pattern at t=0 due to superposition of waves given by y1 and y2 in Figs.7.104(a) and (b) . In Fig. 7.104 (c ) , N is a node and A and antinode . At this instant say t=0 , instantaneous velocity of points on the string named as A
View SolutionA man leaves his home early in the morning to have a walk. He arrives at a junction of roads A and B as shown in figure. He takes the following steps in later journies :
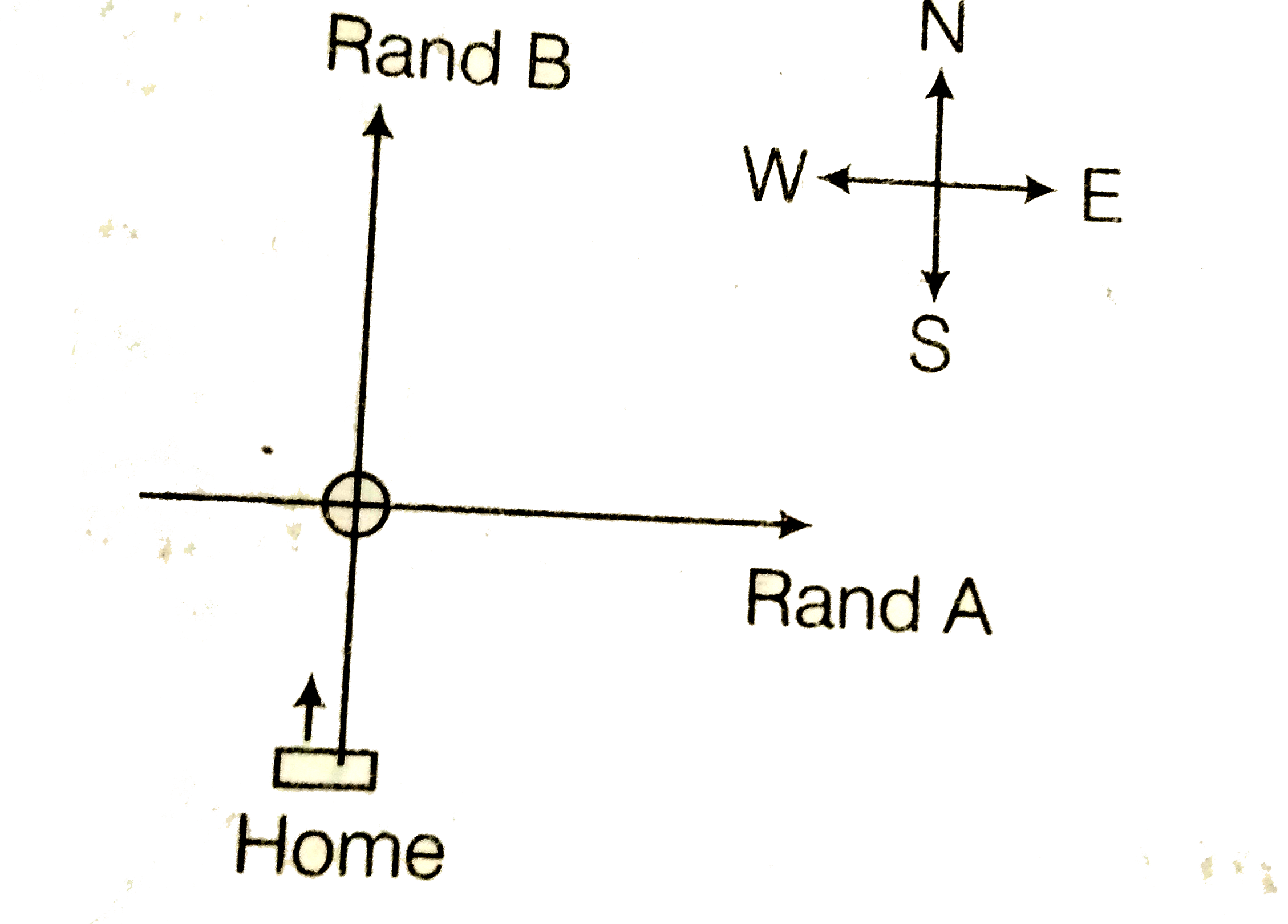
(i) 1 km in North direction.
(ii) Changes direction and moves in North-East direction for 2√2 km.
(iii) Changes direction and moves Southwards for distance of 2 km.
(iv) Finally he changes the direction and moves in South-East direction to reach road A again.
Visible/invisible path The path traced by the man in the direction parallel to road A and road B is called invisible path, the remaining path is called visible.
Visible points The point about which the man changes direction are called visible points, except the point from where he changes direction last time.
Now if roads A and B are taken as X-asix and Y-axis, then visible point representing the graph of y = f(x).
If f(x) is periodic with period 3, then f(19) is
View SolutionA particle of mass m=1.6×10−27 kg and charge q=1.6×10−19C enters a region of uniform magnetic field of stregth 1T along the direction shown in figure. The speed of the particle is 107m/s

a. The magnetic field is directed along the inward normal to the plane of the paper. The particle leaves the region of the fiedl at the point F. Find the distasnce EF and the angle theta.
b. If the direction of the field is along the outward normal to the plane of the paper find the time spent by the particle in the regin of the magnetic field after entering it at E.
View Solution
