A mass M moving with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
a. is zero
b. remains constant
c. goes on increasing
d. goes on decreasing
The correct Answer is:b
To find the angular momentum of a mass M moving with a constant velocity v parallel to the X-axis with respect to the origin, we can follow these steps:
Step 1: Understand the Setup
Consider a mass M moving along the X-axis at a constant velocity v. Let's denote the position of the mass at any time t as (x,0), where x=vt. The distance from the origin to the mass is given by r=x.
Step 2: Define the Angular Momentum
The angular momentum L of a particle with respect to a point (in this case, the origin) is given by the formula:
L=r×p
where p is the linear momentum of the mass, defined as:
p=M⋅v
Step 3: Calculate the Perpendicular Distance
The angular momentum can also be expressed in terms of the perpendicular distance from the line of motion to the point about which we are calculating the angular momentum. Since the mass is moving parallel to the X-axis, the perpendicular distance r_{\perpendicular} from the origin to the line of motion is simply the Y-coordinate of the mass, which is 0 in this case. However, if we consider the mass to be at a distance r1 from the origin, we can express the perpendicular distance as:
r_{\perpendicular} = r_1 \sin(\theta)
where θ is the angle between the position vector and the velocity vector.
Step 4: Express Angular Momentum
Substituting the values into the angular momentum formula, we have:
L = M \cdot v \cdot r_{\perpendicular}
Since the perpendicular distance remains constant as the mass moves along the X-axis, we can conclude that:
L=M⋅v⋅r1sin(θ)
Step 5: Conclusion
Since both the mass M and the velocity v are constant, and the perpendicular distance does not change as the mass moves, the angular momentum L remains constant with respect to the origin. Therefore, the angular momentum of the mass M moving with a constant velocity parallel to the X-axis is constant.
Final Answer
The angular momentum L with respect to the origin is constant.
---
Consider a mass M moving along the X-axis at a constant velocity v. Let's denote the position of the mass at any time t as (x,0), where x=vt. The distance from the origin to the mass is given by r=x.
The angular momentum L of a particle with respect to a point (in this case, the origin) is given by the formula:
L=r×p
where p is the linear momentum of the mass, defined as:
p=M⋅v
The angular momentum can also be expressed in terms of the perpendicular distance from the line of motion to the point about which we are calculating the angular momentum. Since the mass is moving parallel to the X-axis, the perpendicular distance r_{\perpendicular} from the origin to the line of motion is simply the Y-coordinate of the mass, which is 0 in this case. However, if we consider the mass to be at a distance r1 from the origin, we can express the perpendicular distance as:
r_{\perpendicular} = r_1 \sin(\theta)
where θ is the angle between the position vector and the velocity vector.
Substituting the values into the angular momentum formula, we have:
L = M \cdot v \cdot r_{\perpendicular}
Since the perpendicular distance remains constant as the mass moves along the X-axis, we can conclude that:
L=M⋅v⋅r1sin(θ)
Since both the mass M and the velocity v are constant, and the perpendicular distance does not change as the mass moves, the angular momentum L remains constant with respect to the origin. Therefore, the angular momentum of the mass M moving with a constant velocity parallel to the X-axis is constant.
The angular momentum L with respect to the origin is constant.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - EQUILIBRIUM OF A RIGID BODY13videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - MOMENT OF INERTIA7videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - MOTION OF CENTRE OF MASS10videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPERSEXERCISE - All Questions150videos
PRACTICE PAPERS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason10videos
THERMAL PROPERTIES OF MATTER
Similar Questions
A particle moves with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
View SolutionStatement - 1 : A particle moves with a constant velocity parallel to the x-axis. Its angular momentum w.r.t. the origin will remains constant.
Because
Statement - 2 : Angular momentum is defined as →L=→r×→PView SolutionA mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Its angular momentum with respect to the origin.
View SolutionA particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is
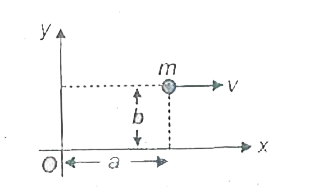 View Solution
View SolutionA body of mass m is moving with a constant velocity along a line parallel to the x-axis, away from the origin. Calculate its angular momentum with respect to the origin?
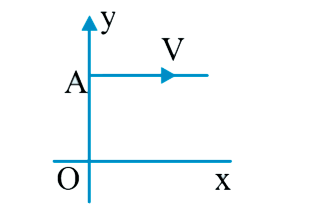 View Solution
View SolutionA particle of mass m moves in the XY plane with constant velocity v along the straight line PQ as shown in the figure. Its angular momentum with respect to origin O is(θ is angle between→v and x-axis)
 View Solution
View SolutionThe time dependence of the position of a particle of mass m = 2 is given by →r(t)=2tˆi−3t2ˆj Its angular momentum, with respect to the origin, at time t = 2 is :
View SolutionThe time dependence of the position of a particle of mass m = 2 is given by →r(t)=2tˆi−3t2ˆj Its angular momentum, with respect to the origin, at time t = 2 is :
View SolutionIf the particle of mass m is moving with constant velocity v parallel to x-axis in x-y plane as shown in (figure), Find its angular momentum with respect of origin at any time t.
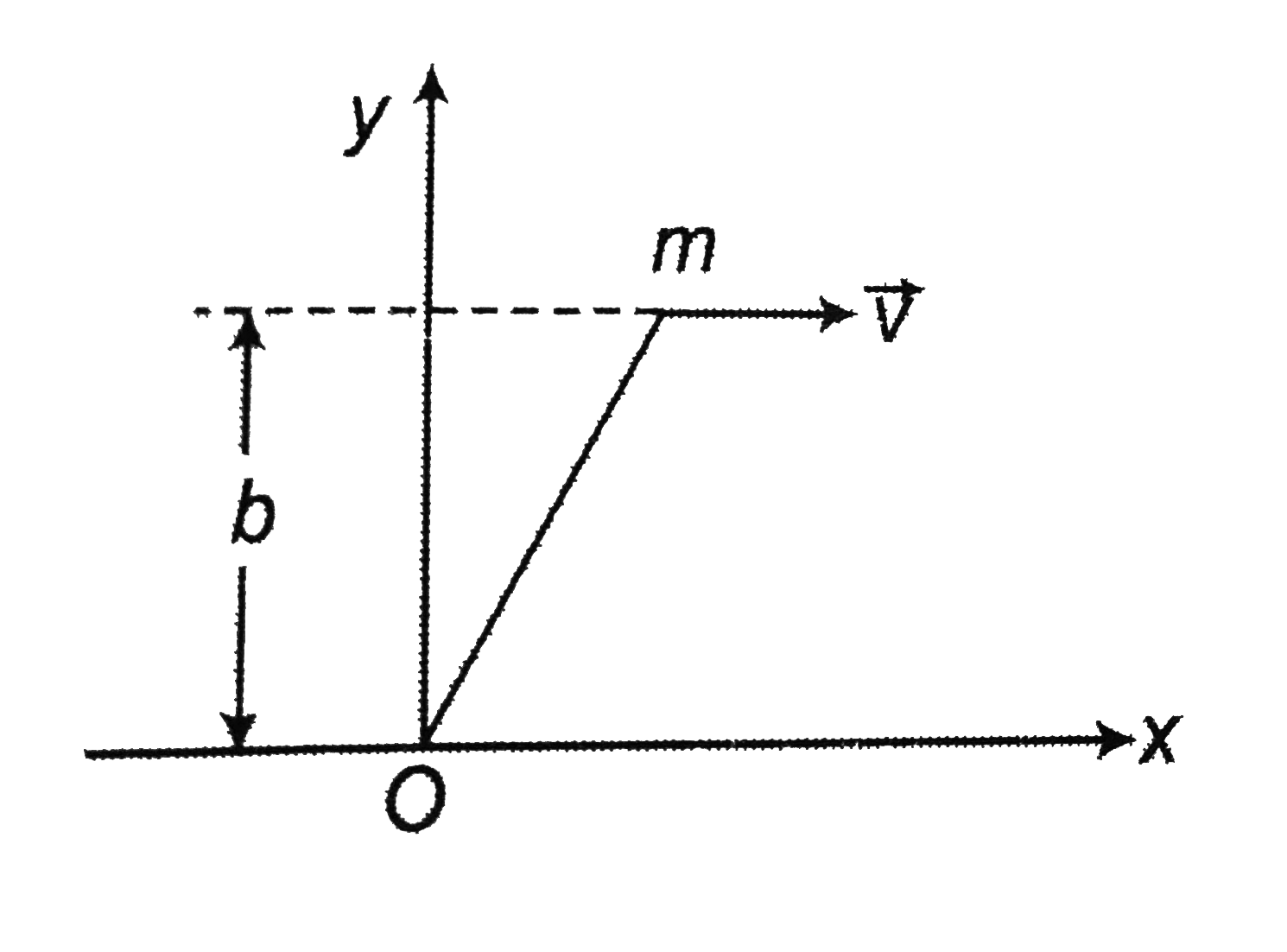 View Solution
View SolutionA solid sphere is rotating with a constant angular velocity about an axis touching the surface. Its angular momentum will be:
View Solution

